数学焦点三角形求法（206021高中数学双曲线中的焦点三角形）

双曲线上的点与两个焦点F₁、F₂构成了焦点三角形。

例1、过双曲线

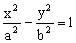
（a>0，b>0）的焦点F₁的弦AB长为m，另一焦点为F₂，则△ABF₂的周长为

A.4a

B.4a 2m

C.

D.

分析：根据双曲线的定义，在双曲线的焦点三角形中，

，

=2a，这是焦点三角形中的一个很重要的结论，从而求出△

的周长。

解：根据双曲线的定义，设F₁、F₂分别是双曲线的左、右焦点，则，

，所以

。因此，△ABF₂的周长为4a 2m，故选B。

例2、设椭圆

和双曲线

的公共焦点为F₁、F₂，P为两曲线的一个交点，则cos∠F₁PF₂的值等于

A.

B.

C.

D.

分析：充分应用椭圆、双曲线的定义，求出焦半径，在双曲线的焦点三角形中，利用余弦定理，从而求出cos∠F₁PF₂的值。

解：由题意，不妨设点P在双曲线的右支上，则在椭圆中，

，在双曲线中，

，所以

，

。又

，故在焦点三角形中，cos∠

，因此，选B。

例3、

是双曲线

的两个焦点，点P在双曲线上且满足

=32，则∠

=____________。

解：不妨假设点P在双曲线的右支上，则

，所以

在焦点三角形中，cos∠

，故∠=90°。

例4、已知双曲线

的两个焦点分别为F₁、F₂，点P在双曲线上且满足∠F₁PF₂=60°，则△F₁PF₂的面积是_________。

解：不妨假设点P在双曲线的右支上，则

由题意知

即

，所以

，因此，

。

例5、过双曲线的一个焦点作垂直于实轴的弦PQ，点是另一个焦点，若

=

，则双曲线的离心率等于_________。

解：设、分别是双曲线的左、右焦点，由题意知在焦点三角形

中，

，

，又

，故有

。

例6、若已知双曲线

的左、右焦点分别为F₁、F₂，左准线为l，能否在双曲线的左支上求一点P，使

是P到l的距离d与

的等比中项？若能，请求出P点的坐标；若不能，请说明理由。

解：由题意，

，即

，又

，所以

。

根据双曲线的定义知，

，因此

，

。

故

，这与点P、、构成焦点三角形矛盾，所以双曲线的左支上不存在点P，使是P到l的距离d与的等比中项。

--END--

,