指数分布公式推导（4.1指数运算）

指数运算:

1.指数幂运算的原则与技巧。

(1)负指数幂化为正指数幂的倒数

(2)底数是小数的,要先化成分数;底数是带分数的,要先化成假分数,然后要尽可能用幂的形式表示,便于利用指数幂的运算性质.

注意:化简的结果不能同时含有根式和分数指数，也不能既含有分母又含有负指数.

2.解决条件求值问题的一般方法--整体代换法将已知条件或所求代数式进行恰当的变形，从而通过“整体代换法”求出代数式的值常用的变形公式如下:

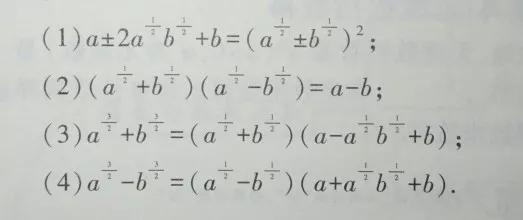
3.记忆口决:

有理数的指数幂，运算法则要记住。

指数加减底不变，同底数幂相乘除。

指数相乘底不变，幂的乘方要清楚。

积商乘方原指数，换底乘方再乘除。

非零数的零次幂，常值为 1不糊涂。

负整数的指数幂，指数转正求倒数。

看到分数指数幂，想到底数必非负。

乘方指数是分子，根指数要当分母。

看到分数指数幂，想到底数必非负。

乘方指数是分子，根指数要当分母。