维数定理及证明（给出实数可数定理）

本文是上期文章预告过的，上期文章给出了实数集可数定理及其第二个证明——等差数列法，现在给出其第三个证明——基数减少法。这个证明是我对自己以前发表过的基数减少法的最新修订，本质是一样的。

所谓基数减少法，就是将开区间 的全体小数任意的一个个减去并编号，直至将开区间 的全体小数减少到零个，并使开区间 的全体小数与自然数集建立 1-1 对应；以此证明实数可数定理。详情如下：

证. 因为任意位小数集如 1 位小数集的不等式链：

都是有小数序列和大小关系的；

所以有实数集

其中 是开区间 的任意的第个小数；例如可以有 ，也可以有 ，等等；不同的排列，就有不同的小数值。中的变量也是等于一个个小数的。

设开区间 全体小数的连续统基数为 ;

因为 ；

所以。

这就是基数被一个个减少到零个，这就是基数减少法的算术；这就相当于把个小数一个个的随机取出并编号（用自然数编号），直至小数被全部取完；如：

因为集合 的连续统基数为 ；

所以共有 个小数都可以作为第一次被取出的小数 ，共有 个小数都可以作为第二次被取出的小数 ，…… ， 最终只有 个小数可以作为第 次被取出的小数；

所以集合 的 个小数共有

种不同的取数并编号的方法，也就是共有 种不同的基数减少法，每一种都可以建立集合 的全体小数与自然数集

的 1-1 对应：

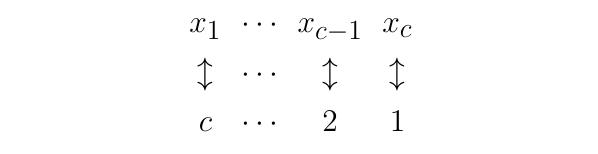
因此就证明了集合 是可数的，就证明了实数集是可数的。

证毕

参考文献

[1] 推翻实数不可数假定理，提出实数可数定理， 及等差数列法证明。《今日头条》，侯拉 数学，2022-04-23，

[2] 侯小山，实数集可数定理，《数学学习与研究》2014.9，东北师范大学主管，第 110-111页。

下期预告

下期文章将给出实数集可数定理的第四个证明——对称证明法，敬请期待。