高中数学有关三角函数的知识（高三数学知识点之三角函数）

考试内容：

角的概念的推广．弧度制．

任意角的三角函数．单位圆中的三角函数线．同角三角函数的基本关系式.正弦、余弦的诱导公式．

两角和与差的正弦、余弦、正切．二倍角的正弦、余弦、正切．

正弦函数、余弦函数的图像和性质．周期函数．函数y=Asin(ωx φ)的图像．正切函数的图像和性质．已知三角函数值求角．

正弦定理．余弦定理．斜三角形解法．

考试要求：

（1）理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算．

（2）掌握任意角的正弦、余弦、正切的定义；了解余切、正割、余割的定义；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；了解周期函数与最小正周期的意义．

（3）掌握两角和与两角差的正弦、余弦、正切公式；掌握二倍角的正弦、余弦、正切公式．

（4）能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明．

（5）理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx φ)的简图，理解A.ω、φ的物理意义．

（6）会由已知三角函数值求角，并会用符号arcsinx\arc-cosx\arctanx表示．

（7）掌握正弦定理、余弦定理，并能初步运用它们解斜三角形．

（8）“同角三角函数基本关系式：sin2α cos2α=1，sinα/cosα=tanα,tanα•cosα=1”．

三角函数 知识要点

1. ①与α（0°≤α＜360°）终边相同的角的集合（角α与角β的终边重合）：{β|β=k*360° α，k∈Z}

②终边在x轴上的角的集合： {β|β=k*180°，k∈Z}

③终边在y轴上的角的集合：{β|β=k*180° 90°，k∈Z}

④终边在坐标轴上的角的集合： {β|β=k*90°，k∈Z}

⑤终边在y=x轴上的角的集合：{β|β=k*180° 45°，k∈Z}

⑥终边在轴上y=-x轴上的角的集合：{β|β=k*180°-45°，k∈Z}

⑦若角α与角β的终边关于x轴对称，则角α与角β的关系：α=360°k-β

⑧若角α与角β的终边关于y轴对称，则角α与角β的关系：α=360°k 180°-β

⑨若角α与角β的终边在一条直线上，则角α与角β的关系：α=180°k β

⑩角α与角β的终边互相垂直，则角α与角β的关系：α=360°k β±90°

2. 角度与弧度的互换关系：360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′

注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.

、弧度与角度互换公式： 1rad＝180°/π≈57.30°=57°18ˊ． 1°＝π/180ι≈0.01745（rad）

3、弧长公式：ι=|α|·r. 扇形面积公式：s扇形=1/2lr=1/2|α|·r²

4、三角函数：设α是一个任意角，在α的终边上任取（异于原点的）一点P（x,y）P与原点的距离为r，则sinα=y/r ； cosα=x/r ；tanα=y/x ； cotα=x/y ；secα=r/y ；. .

5、三角函数在各象限的符号：（一全二正弦，三切四余弦）

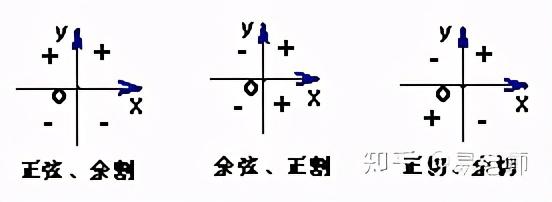
6、三角函数线

正弦线：MP; 余弦线：OM; 正切线： AT.

7. 三角函数的定义域：

8、同角三角函数的基本关系式：sinα/cosα=tanα cosα/sinα=cotα

tan²α cot²α=1 secα·sinα=1 secα·cosα=1

sin²α cos²α=1 sec²α-tan²α=1 csc²α-cot²α=1

9、诱导公式：

“奇变偶不变，符号看象限”

三角函数的公式：（一）基本关系

公式组二

公式组三

公式组四

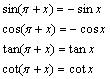
公式组五

公式组六

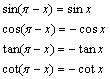
（二）角与角之间的互换

公式组一

cos（α β）=cosαcosβ-sinαsinβ

cos（α-β）=cosαsinβ sinαcosβ

sin(α β )=sinαcosβ cosαsinβ

sin（α-β）=sinαcosβ-cosαsinβ

tan（α β）=（tanα tanβ）/（1-tanαtanβ）

tan（α-β）=（tanα-tanβ）/（1 tanαranβ）

公式组二

sin2α=2sinαcosα

cos2α=cos²α-sin²α=2cos²α-1=1-2sin²α

tan2α=2tanα/（1-tan²α）

sinα/2=±√cosα/2

cosα/2=±√（1 cosα）/2

tanα/2=±√√（1-cosα）/（1 cosα）=sinα/（1 cosα）=（1-cosα）/sinα

公式组三

sinα=（2tan²α/2）/（1 tan²α/2）

cosα=（1-tan²α/2）/（1 tan²α/2）

tanα=（2tanα/2）/（1-tan²α/2）

公式组四

sinαcosβ=1/2[sin（α β） sin（α-β）]

cosαsinβ=1/2[sin（α β）-sin（α-β）]

cosαsinβ=1/2[cos（α β） cos（α-β）]

sinαsinβ=-1/2[cos（α β）-cos（α-β）]

sinα sinβ=2sin[（α β）/2]cos（α-β）/2

sinα-sinβ=2cos[（α β）/2]sin（α-β）/2

cosα cosβ=2cos[（α β）/2]cos(α-β）/2

cosα-cosβ=-2sin[（α β）/2]sin（α-β）/2

公式组五

cos（1/2π-α）=sinα

sin（1/2π-α）=cosα

tan（1/2π-α）=cotα

cos（1/2π α）=-sinα

tan（1/2π α）=-cotα

sin（1/2π α）=cosα

sin15°=cos75°=（√6-√2）/4，sin75°=cos15°=√6 √2）/4，tan15°=cot75°=2-√3，tan75°=cot15°=2 √3

10. 正弦、余弦、正切、余切函数的图象的性质：

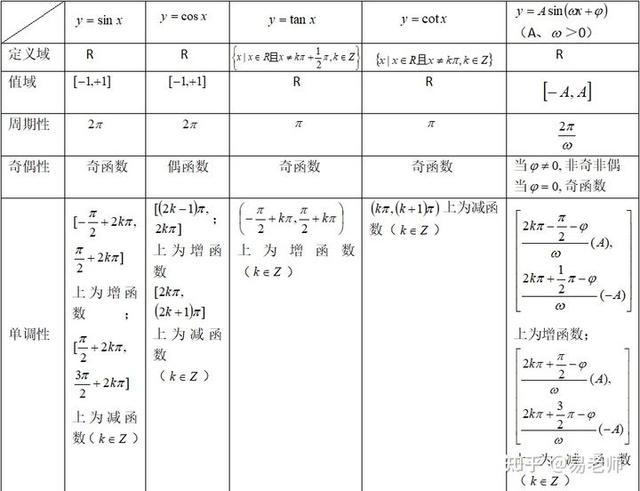
注意：①y=-sinx与y=sinx的单调性正好相反；y=-cosx与y=cosx的单调性也同样相反.一般地，若y=f（x）在[a,b]上递增（减），则y=-f（x）在[a.b]上递减（增）.

②y=|sinx|与y=|cosx|的周期是π.

③y=sin（ωx φ）或y=cos（ωx φ）（ω≠0）的周期T=2π/|ω|.

y=|tanx/2|的周期为2π（T=π/|ω|=>T=2π，如图，翻折无效）.

④y=sin（ωx φ）的对称轴方程是x=kπ π/2（k∈Z），对称中心（kπ，0）；y=cos（ωx φ）的对称轴方程是x=kπ（k∈Z），对称中心（kπ 1/2π，0）；y=tan（ωx φ）的对称中心（kπ/2,0）.y=cos2x→原点对称→y=-cos（-2x）=-cos2x

⑤当tanα·tanβ=1，α β=kπ π/2（k∈Z）；tanα·tanβ=-1·α-β=kπ π/2（k∈Z）.

⑥y=cosx与y=sin（x π/2 2kπ）是同一函数,而是偶函数，则y=（ωx φ）=sin（ωx kπ 1/2π）=±cos（ωx）.

⑦函数y=tanx在R上为增函数.（×） [只能在某个单调区间单调递增. 若在整个定义域，y=tanx为增函数，同样也是错误的].

⑧定义域关于原点对称是f（x）具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原点对称（奇偶都要），二是满足奇偶性条件，偶函数：f（-x）=f（x）*，奇函数：f（-x）=-f（x）

奇偶性的单调性：奇同偶反. 例如：ttanx是奇函数，y=tan（x 1/3π）是非奇非偶.（定义域不关于原点对称）

奇函数特有性质：若0∈x的定义域，则f（x）一定有f（0）=0.（0不属于x的定义域，则无此性质）

⑨y=sin|x|不是周期函数；y=|sinx|为周期函数（T=π）；

y=cos|x|是周期函数（如图）；y=|cosx|为周期函数（T=π）；

y=|cos2x 1/2|的周期为π（如图），并非所有周期函数都有最小正周期，例如：y=f（x）=5=f（x k），k∈R .

⑩ y=αcosα bsinβ=√（a² b²）*sin（α β） cosβ=b/a有√（a² b²）≧|y|.

11、三角函数图象的作法：

１）、几何法：

２）、描点法及其特例——五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）.

３）、利用图象变换作三角函数图象．

三角函数的图象变换有振幅变换、周期变换和相位变换等．

函数y＝Asin（ωx＋φ）的振幅|A|，周期T=2π/|ω|，频率f=1/T=|ω|/2π，相位ωx φ；初相φ（即当x＝0时的相位）．（当A＞0，ω＞0 时以上公式可去绝对值符号），

由y＝sinx的图象上的点的横坐标保持不变，纵坐标伸长（当|A|＞1）或缩短（当0＜|A|＜1）到原来的|A|倍，得到y＝Asinx的图象，叫做振幅变换或叫沿y轴的伸缩变换．（用y/A替换y）

由y＝sinx的图象上的点的纵坐标保持不变，横坐标伸长（0＜|ω|＜1）或缩短（|ω|＞1）到原来的倍，得到y＝sinω x的图象，叫做周期变换或叫做沿x轴的伸缩变换．(用ωx替换x)

由y＝sinx的图象上所有的点向左（当φ＞0）或向右（当φ＜0）平行移动｜φ｜个单位，得到y＝sin（x＋φ）的图象，叫做相位变换或叫做沿x轴方向的平移．(用x＋φ替换x)

由y＝sinx的图象上所有的点向上（当b＞0）或向下（当b＜0）平行移动｜b｜个单位，得到y＝sinx＋b的图象叫做沿y轴方向的平移．（用y (-b)替换y）

由y＝sinx的图象利用图象变换作函数y＝Asin（ωx＋φ）（A＞0，ω＞0）（x∈R）的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象延x轴量伸缩量的区别。

4、反三角函数：

函数y＝sinx，（x∈[-π/2，π/2]）的反函数叫做反正弦函数，记作y＝arcsinx，它的定义域是［－1，1］，值域是[-π/2，π/2]．

函数y＝cosx，（x∈［0，π］）的反应函数叫做反余弦函数，记作y＝arccosx，它的定义域是［－1，1］，值域是［0，π］．

函数y＝tanx，（x∈[-π/2，π/2]）的反函数叫做反正切函数，记作y＝arctanx，它的定义域是（－∞，＋∞），值域是(-π/2，π/2)．

函数y＝ctgx，［x∈（0，π）］的反函数叫做反余切函数，记作y＝arcctgx，它的定义域是（－∞，＋∞），值域是（0，π）．

高三数学补习班：「链接」

,