几何精讲线面夹角例题（立体几何经典习题之线面夹角）

线面夹角习题

1. 面面垂直证明

用于面面平行的常用方法:证明一个平面经过另一个平面的垂线。

该题中:

∵ABCD为菱形 ∴AC⊥BD

又∵BE⊥平面ABCD,AC⊂平面ABCD

∴AC⊥BE 则AC⊥平面BED

∵AC⊂平面AEC ∴平面AEC⊥平面BED

2. 求线面夹角正弦值

求解线面夹角一般有两种方法，即几何法和相量法。

• 几何法

（1）寻找过斜线上一点与平面垂直的直线。

（2）连接垂足和斜足得到斜线在平面上的射影，斜线与其射影的锐角或直角即为所求角。

（3）把该角归结到某个三角形中，通过解三角形求解。

• 相量法

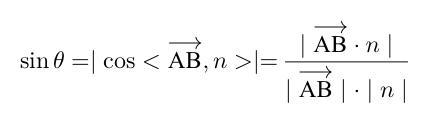
向量求解公式

其中AB为平面α的斜线，n为平面α的法向量，θ为斜线AB与平面α所成的角。

从该题的图形来看，几何法会略显复杂一些，我们给大家带来向量的求解方法，有兴趣的同学可以尝试挑战几何法。

向量法求解答案

该题中第一个问较为简单，只需掌握基本线面关系定理即可求解。在第二个问中，求解线面夹角、面面夹角问题，是高考的热门考点，需要考生在掌握基本求解方法的基础上，熟练应用的解题过程中。例如几何法求解，需要在平时一定题量累计的基础上，才能在考试时快速做出垂线，找出夹角。

写在最后，立体几何的难点在于线面、面面夹角，想要拿到满分，这一部分的题量累积是必不可少的。