小升初几何专项练习题基础（小升初经典几何练习题）

题目：在上图的梯形ABCD中，CD的长是AB长的2倍，BC=5厘米，DE=8 厘米，则梯形ABCD的面积是多少?

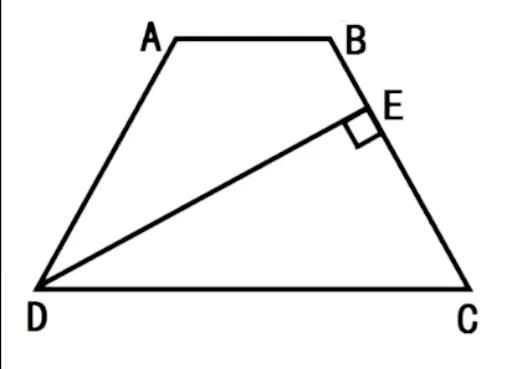
方法一:纯小学方法，等高模型

连接BD

S△BCD=BC×DE÷2=5×8÷2=20cm^2

S△ABD和S△DCB同高，AB=1/2DC

等高模型，高相等的两个三角形，面积比等于底之比。

S△ABD=1/2S△DCB=1/2×20=10cm^2

S梯形ABCD=S△ABD S△DCB

=10 20=30cm^2

方法二:初中中位线知识解答

延长DA、CB至顶点相交F，由于线段AB平行且等于CD的一半。所以可以得到AB为新构造三角形CDF的中位线，BF=BC=5.三角形CDF面积是（5 5）*8/2=40cm^2

根据△中位线定理.面积比等于相似比的平方，可以得到上面的△ABF面积占整个△CDF面积的1/4，那就是40×1/4=10，所以梯形ABCD面积是三角形CDF的面积-三角形ABF的面积40-10=30cm^2