梳状函数和矩形函数的卷积怎么求（由它可构造不可积的有界导函数）

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，e^iπ 1=0，哆嗒数学网翻译组成员。

校对，donkeycn

关注哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

上回我们写了一篇关于康托集的文章，它是一个将小与大统一起来的有趣的数学空间。

说小是因为它的长度只有零，但是说大是因为它本身是个不可数的集合。

一旦一个数学家着手处理一个数学对象，直觉上第一步便是试着摆弄它，然后看看会发生什么。这使我们得到了胖康托集（编者注：Fat Cantor Set 正规教材上译为类康托集，但是本文要显示他比康托集“肥硕”于是就这样翻译了）。

当有人提起康托集时，他们指的是标准三分康托集，也就是我之前提到的那个康托集。

这个集合的构造是通过将区间[0,1]中间三分之一的部分移除，只留下区间[0,1/3] 和 [2/3,1]。

然后将剩下的每个区间再去掉各自的中间三分之一，这样的操作一直重复下去。

令人惊奇的是，这样的操作使得这个区间还有一些东西留下，却没有长度。

第一个能想到的符合逻辑的操作就是将康托集移除三分之一这个比例换成其他的比例。

如果我们只移除每个区间中间的四分之一会产生什么样的结果呢？

我们同样从区间[0,1]开始操作。

第一步，我们只留下区间[0,3/8] 和 [5/8,1]。

然后我们继续移除每个区间中间四分之一的区间（移除的区间长度变为3/32）。

你可能会认为会有更多的东西被留下，因为我们每步移除了更短的区间，但这个想法是不对的。

如果你将所有移除的区间长度都加在一起，我们仍旧得到1。

这个康托集实际上并没有比我们之前那个集合更有趣。

当然我们也没有变得更不幸运。

如果我们保证每次移除区间所用的比例都是一样的，那我们总能得到移除的区间长度总和为1。

当然有很多方法区别那些移除中间三分之一，四分之一，或者任何一个比例的康托集，但是现在我们准备试着对康托集做很不一样的操作。

第二件我们可以做的事情是改变每次移除区间时所用的比例。

我们将再次从区间[0,1]中移除中间四分之一的区间，这样我们留下区间[0,3/8]和[5/8,1]。

但是到了第二步，我们将从每个剩余的区间中移除它中间一个长为十六分之一的区间。

这时候，情况已经发生了些许变化。

之前的时候，我们从每个剩余区间移除了长为三十二分之三的区间，这比起十六分之一稍微长上一些。

在新的构造中，我们将不断改变每一步里剩余区间需要去除的区间长度。

在第一步中，我们移除了初始区间的四分之一。

在第二步中，我们从每个剩余区间移除长为十六分之一的区间，相较于初始区间，共移除了八分之一。

在第三步中，我们每个剩余区间移除了长为六十四分之一的区间，相较于初始区间，共移除了十六分之一。

我们可以继续这样的操作，到了第n步的时候，我们将移除整段区间1/2n 1的长度。

如果这个步骤无限地做下去，我们总共移除的长度将会是1/4 1/8 1/16 …，而它的和则是1/2。

这时候我们的确得到了一些新的东西！

这个结构被称作史密斯-沃尔泰拉-康托集合，或者是胖康托集。

康托集的一维测度是0，这是因为我们移除的区间长度和等于一开始的区间长度，但是胖康托集还留下了一些东西——从整个[0,1]区间里留下整整一半。

那这些是从哪里来的呢？

根据构造过程，胖康托集不包含任何区间。

每当我们看到一个区间，我们都要移除这个区间中的一部分。

某种程度上，有一些长度是被留下了，但不是以我们熟悉的方式留下的。

如果我们试图用手去抓，只能抓到一把灰尘。

康托集挑战了我对小与大的直觉认识。

胖康托集更将我的直觉完全吹散了。

一个没有任何微小片段的一维物体究竟是怎样获得一定长度的？

当然，这样说其实不完全公平。

在区间[0,1]上的所有无理数组成的集合，它的一维测度为1，长到居然与整个区间一样，但是这个听上去并没有那么的违反直觉。

无理数无处不在。

所以，你在数轴上随便一扫，都能扫到无理数。

在数学上，我们把这种情况叫做区间上稠密，或者在所有实数构成的集合中，无论怎么样选择一个子区间，无论有多小，都会包含着无理数。

是否稠密这一问题使得胖康托集变得更奇怪。

胖康托集在[0,1]区间上不是稠密的，而且他们甚至在任何更小的区间上都不是稠密的。

无论你的区间取得多么小，你都能找到一个完整的区间，其中任何一点都不在胖康托集中。

我们将这种情况叫做无处稠密(nowhere dense)。

这样胖康托集的长度是1/2就没什么稀奇的地方了。

事实上，调整每一步需要移除的区间长度，我们可以得到一个按照我们想要的任意长度的康托集。

我们不能得到一个长度为1的胖康托集，但是我们可以得到一个长度趋近于1的胖康托集。

无论我们将胖康托集塑造的多大，他们都不会占满任何一个区间，并且会无处稠密。

那我们可以在哪里看到他们呢？

我第一次遇到康托集的地方就是康托函数，这我提到过了。

康托函数，或者说是魔鬼的楼梯，向我们展示了联系了微分与积分的微积分基本定理的局限性。

事实上胖康托集也能做到这一点。

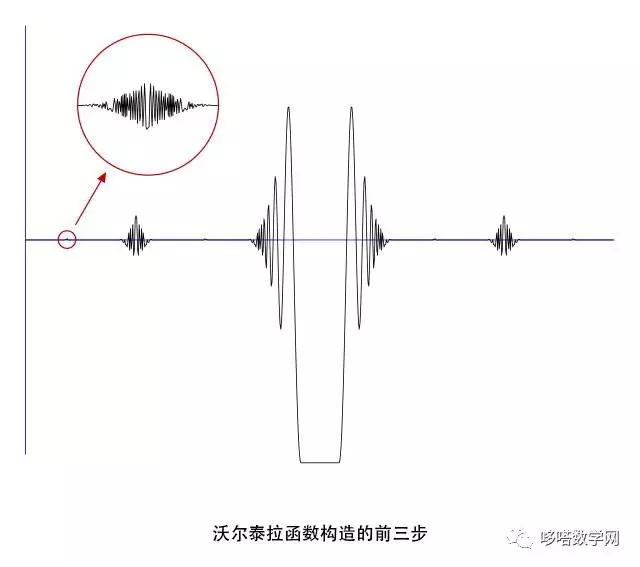
特别地，意大利数学家沃尔泰拉 (Volterra ,1860-1940)利用胖康托集构造了一个可微函数但是导函数不可积。

关注哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

,