支持向量机分类算法（聊聊支持向量机的数学原理）

前言：支持向量机SVM算法，以前用的不多，但是以后肯定会用得到，但是真想搞明白还是有点难度的，参考了许多大牛的文章，总算是把基本的数学原理理解的差不多，公式比较多，通过图文的方式，总算是做了简单的探究

支持向量机是一种分类算法，特别是针对数据集较小的的情况下，往往分类效果比神经网络好

原理：最大特点是构造出最大间距的决策边界，从而提高分类算法的鲁棒性

使用SVM算法的思路：

一：简单情况，线性可分情况，把问题转化为一个凸优化问题，可以用拉格朗日乘子法简化，然后用既有的算法解决

二：复杂情况，线性不可分，用核函数将样本投射到高维空间，使其变成线性可分的情形，利用核函数来减少高纬度计算量。

1，线性可分的情况：

（1）分割超平面与间距

对一个数据集进行分类，构造一个分隔线把圆点和五角星分开，这个分隔线称为分割超平面

从上图可以看出，红线就是最好的分割线，那些离分割超平面最近的点，称之为支持向量，离分隔线最近的点到分隔线的距离就是间距，其中Gap就是两倍的间距

（2）怎么计算间距？

在二维空间中，可以使用方程

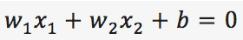
来表示一个超平面

针对高纬度空间，可以转化成一般化的向量形式，即

我们画出与分割超平面平行的两条直线，分别穿过两个类别的支持向量，如下图：

根据点到直线的距离，可以容易地算出支持向量到分隔超平面的距离：

||w||表示w的二范数

我们目的是为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔W=2d的大小，即分类间隔w越大，我们认为这个超平面的分类效果越好。此时，求解超平面的问题就变成了求解分类间隔W最大化的问题，W的最大化也就是d最大化的。

（3）约束条件

问题来了，我们如何判断超平面是否将样本点正确分类？

这个二维平面上有两种点，我们分别对它们进行标记：

红颜色的圆点标记为1，我们人为规定其为正样本；

蓝颜色的五角星标记为-1，我们人为规定其为负样本。

针对上图，我们可以看出，对于红点x,必定满足

对于五角星x，必定满足

因此，针对数据集中所有的样本x,y，如果我们的超平面方程能够完全正确地对样本点进行分类，就会满足下面的方程：

标签为1和-1，我们将约束条件变成一个约束方程

（4）目标函数：

我们的优化目标是是d最大化。我们已经说过，我们是用支持向量上的样本点求解d的最大化的问题的。那么支持向量上的样本点有什么特点呢？

支持样本点分布在超平面

这样，支持向量到达我们要优化的超平面 距离就是1/∥ω∥，间距就是2/∥ω∥现在我们可以将目标函数进一步优化：

我们只关心支持向量上的点。随后我们求解d的最大化问题变成了||w||的最小化问题。进而||w||的最小化问题等效于（加上约束条件）：

这里n是样本点的总个数，缩写s.t.表示"Subject to"，是"服从某某条件"的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题，同时也是支持向量机的基本数学模型。

注：在逻辑回归中使用0和1座位类别标签，而在支持向量机中，我们使用1和-1作为类别标签，其目的都是为了让数学表达式尽量简洁

一句话总结：求解SVM算法，就是在满足约束条件的前提下，求解

的最小值

2，线性不可分

（1）松弛系数

如果针对不可分的数据集，针对可分数据集的方法就失效了，因为无法找到最大间距的分割超平面，

解决办法：引入一个参数，称为松弛系数ξi，然后可以把目标函数变成：

其中N为数据集个数，C为算法参数，约束条件相应地变成：

怎样理解松弛系数？我们可以把ξi理解为数据样本X违反最大间距规则的程度，针对大部分正常的样本，即满足约束条件的样本ξ=0，而对部分违反最大间距规则的样本ξ>0，参数C表示对违反最大间距规则样本的'惩罚'力度，当C比较大的时候，对于违反规则的点的惩罚力度将变得很大，C比较小的时候，对于违反规则的点，其付出的代价不是特别大，一般模型会倾向于允许部分样本违反最大间距规则

其实松弛系数类似逻辑回归中的正则项，目的都是为了纠正过拟合问题，让支持向量机对噪声数据有更强的适应性。

（2）拉格朗日乘子法

拉格朗日乘子法是解决在约束条件下，求函数极值的理想方法，其方法是引入非负系数α作为权重作为约束条件的权重：

针对每一个样本集X,y都有一个αi与之对应，极值处偏导数为0，求L对w，b的偏导数，并等于0：

得到：

怎样求最小值，广泛的应用是SMO(序列最小化算法)

注：最好求解处理的α有个明显特点，即大部分都是0，因为只有那些支持向量所对应的样本直接决定了间距的大小，其他的样本离分隔超平面太远，对间距没什么影响。

（2）核函数

最简单的核函数：我们注意到，L中有

其实它是一个数值，是两个输入特征向量的内积，我们把它称之为核函数，他的物理意义是衡量两个向量的相似性。

为什么要引入核函数？

假设有一个数据集，只有一个特征，是线性不可分，要对这个数据集分类，这时候很难找一个超平面来分隔这个数据集。

为了解决这个问题，我们可以用一定规则把这些无法进行线性分隔的样本映射到更高维度的空间里，在高纬度空间找出分隔超平面，SVM的核函数就是为了实现这种相似性映射。假如我们一个[x]变量，把他变成二维的，就是变成[x,2x**2],此时就变成二维的向量，进行这种特征映射的函数为

相似性函数

这样原来在低纬度运算的，就可以转化为高纬度空间的相似性运算

核函数和相似性函数有什么关系？

相似性函数是映射函数，而核函数定义为特征向量的內积，即

核函数

在实际运算中我们不会计算相似性函数及其映射值，因为这样计算量很大

从二维空间扩展到多维，可以使用某种非线性的方法，让空间从原本的线性空间映射到另一个维度更高的空间，在这个高维的线性空间中，再用一个超平面对样本进行划分，这种情况下，相当于增加了不同样本间的区分度和区分条件。在这个过程中，核函数发挥了至关重要的作用，就是为了实现这种相似性映射，核函数的作用就是在保证不增加算法复杂度的情况下将完全不可分问题转化为可分或达到近似可分的状态。

如下图：

,