直角三角形的内切圆半径怎么算（直角三角形旋转后）

直角三角形ABC，两条直角边AC=5, BC=12，将三角形ABC顺时针旋转90°得到三角形CED， 点O为DE上一点，以O为圆心，OD为半径作一个圆

请问当⊙O和直角三角形ABC的边相切时，这时⊙O的半径是多少？

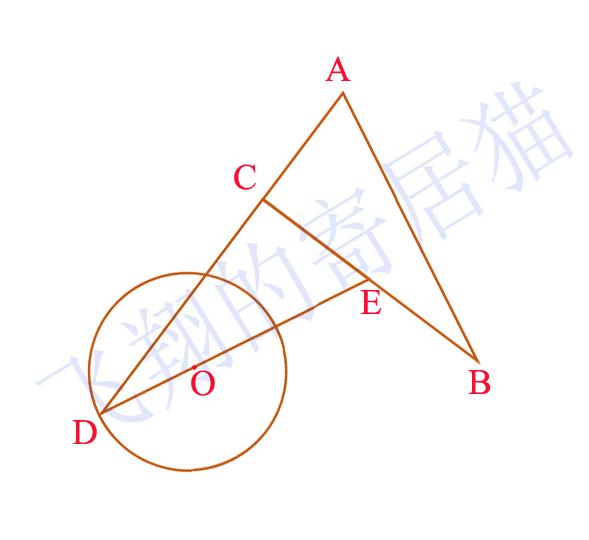
由于O点是在DE上移动变化的，所以我们可以观察下什么时候圆O会与三角形ABC相切。可以发现，和圆相切的边可以是BC或者是AB，而AC是不可能的。很多同学会忽略AB这条边。所以本题应该是有两个答案。

第一种情况，与BC边相切时，假如切点为M，那么连接OM可以得到一个直角三角形OME，由于三角形ABC的三条边通过勾股定理可以得知为5,12,13，所以三角形OME和三角形CDE是相似的，可以得到对应边的比为OM:OE=12:13， OM即为 ⊙O的半径R,得到OE=R13/12,而OE OD=OE R=R13/12 R=13, 解这个方程就可以求出第一种情况的⊙O半径R.

第二种情况，当与AB边相切时，我们把DE延长，假如交AB于点N，那么DN⊥AB，而圆心O在DN上，所以N点即为切点。所以此时DN=2R，而DN=EN 13，所以求出EN是关键，而EN通过相似比，EN:EB=5:13,而EB=12-5=7，从而求出EN=35/13，代入EN 13=2R,即可求出第二种情况的R。

抛砖引玉，大家有好的思路一起来畅所欲言！