二倍角余弦正切公式推导（高中数学正余二倍角公式的变式及其应用）

在三角函数的学习过程中，我们不仅要熟记一些常见的三角公式，而且要熟悉其变化形式，尤其是常用公式的变形公式。下面通过对二倍角的正余弦公式的变形使用，加以说明。

变形一：

例1、求

的值。

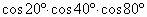
解析：原式

说明：本题中利用变形公式

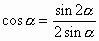
，使得问题得以巧解，简洁明快。另本题也可进行倍角变换，有如下解法：

原式

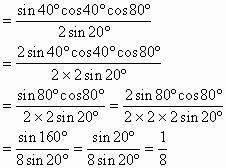
变形二、

以及

例2、求证：

证明：左边

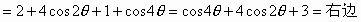
例3、已知

，求

的值。

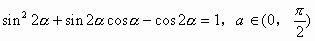
解析：由

得

所以

即

因为

所以

所以

即

所以

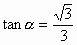
所以

说明：本题通过利用升幂公式：

，使得已知条件得以因式分解，进而使问题获解。

变形三：根据诱导公式，有

，于是有二倍角公式的如下变形

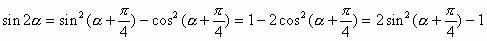
例4、已知

的值。

解析：因为

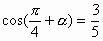
所以

所以

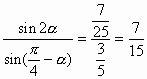
例5、已知

，求

的值。

解析：

所以

因为

，所以

所以

变形四：对于正切二倍角公式：

，通常也有如下变形：

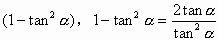
等等

例6、证明：万能公式：（1）

。

证明：由二倍角公式：

，得

，于是：欲证公式

成立，即证明公式

成立。（注：这里应注意

为欲证的另一公式

！）

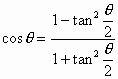
将上述公式的右边切化弦：

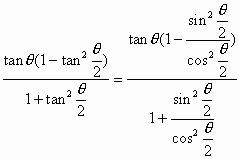
=左边，命题得证。

说明：在这个公式的证明过程中，我们还得到了另一个非常重要的副产品，即

，真所谓“一石二鸟”之举！

--END--

,