平面直角坐标系初二数学（七年级数学平面直角坐标系）

平面直角坐标系知识点

一、平面直角坐标系

1.平面直角坐标系：(1)在平面内两条有公共点并且互相垂直的数轴就构成了平面直角坐标系，通常把其中水平的一条数轴叫横轴或轴，取向右的方向为正方向;铅直的数轴叫纵轴或轴，取向上的方向为正方向;两数轴的交点叫做坐标原点。

(2)建立了直角坐标系的平面叫坐标平面.x轴和y轴把坐标平面分成四个部分，称为四个象限，按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限，如图所示.

说明：两条坐标轴不属于任何一个象限。

2.点的坐标：

对于平面直角坐标系内任意一点P，过点P分别向x轴和y轴作垂线，垂足在x轴，y轴对应的数a,b分别叫做点P的横坐标，纵坐标，有序数对(a，b)叫做P的坐标。

3.点与有序实数对的关系：坐标平面内的点可以用有序实数对来表示，反过来每一个有序实数对应着坐标平面内的一个点，即坐标平面内的点和有序实数对是一一对应的关系。

二、特殊点的坐标特征

1. 各象限内点的坐标的符号特征如下表：

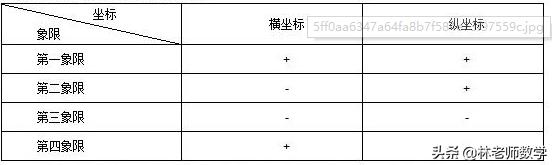
说明：根据各象限内点的坐标的符号特征，一直点的坐标可以判断其位置；反之，已知点的位置也可以判断其横、纵坐标的特点。

2. 若点P在x轴上，则横坐标a为任意实数，b=0；若点P在y轴上，则纵坐标b为任意实数，a=0.

3. 设P的坐标（a，b），若a=b，则点P在第一、第三象限夹角平分线上时；若a=-b，点P在第二、第四象限的角平分线上。

4. 设P（a，b），q（c，d），若a=c≠0且b≠d，则pq// y轴；若b=d≠0且a≠c，则pq // x轴。

6. 在同一直线上的两个点A（a,0）、B(b,0)之间的距离为AB=|b-a|;

平面直角坐标系中两点间距离公式

两点的距离公式和中点公式

1.对于数轴上的两点，设它们的坐标分别为，，则的距离为，的中点的坐标为.

由于表示数轴上两点与的距离，所以在解一些简单的含绝对值的方程或不等式时，常借助于数形结合思想，将问题转化为数轴上的距离问题加以解决.例如，解方程时，可以将问题看作在数轴上求一点，使它到，的距离之和等于.

2.对于直角坐标系中的两点，设它们的坐标分别为，，则两点的距离为，的中点的坐标满足，.

两点的距离公式和中点公式是解析几何中最基本、最常用的公式之一，要求同学们能熟练掌握并能灵活运用.

常见考法

(1)由点的位置确定点的坐标，由点的坐标确定点的位置;(2)求某些特殊点的坐标。

(1)求点的坐标时，容易将横、纵坐标弄反，还容易忽略坐标符号;(2)思考问题不周，容易出现漏解。(如点P到x轴的距离为1，这里点P的纵坐标应当是，而不是1)。

· 平面直角坐标系典型例题

题目

【典型例题】(2010江苏常州)点p(1,2)关于x轴的对称点p1的坐标是 ，点p(1,2)关于原点O的对称点P2的坐标是 。