高考数学二面角大题及答案（难度很大的几个三视图题目）

前面给大家讲了三视图还原--内部直线法，但是有的题目无法用内部直线法来做。

上面这个题目是2015年全国二卷第六题，用内部直线法好像并不好做。

这里需要用到的就是正方体或长方体内部截取法。

因为三个视图都是正方形，所以我们先画一个正方体。

正视图看到的是ABB'A'这个面，正视图中直线是左下右上，所以也就是连接A'B这两点。

侧视图看到的是ADD'A'这个面，侧视图中直线是左上右下，所以连接DA'这两个点。

俯视图看到的是ABCD这个面，俯视图中直线是左上右下，也就是连接BD这两个点。

所以原几何体就是正方体切去A-BDA'三棱锥剩下的部分，体积之比就好求了。

-------------------------------------------------------------------------------------------------

首先，三视图里面没有实线，只有一条虚线，所以不能用内部直线法，我们来试一试内部截取法。

从每个三视图顶点位置，其实我们可以看出来这个几何体也是从正方体中截出来的。

接下来，我们一点点地分析：

因为正视图右边有一条竖直的线，所以在正方体的BC棱和B'C'棱需要各取一点连线（随便取），正视图右边才能看到一条竖直的线。

又因为俯视图只能看到右上角的一个点，所以正视图中右边直线应该是C和C'的连线。

俯视图左下角有一点，所以需要从正方体AA'上和CC'上各取一点（随便取），才会出现俯视图中右下边的斜线。

又因为正视图看到的左上角是一个点，所以AA'上只能取A这个点。

正视图看到一条虚线，虚线下段其实就是C'点，上端在正视图上边中点，需要在EF上任取一点，正视图才会有倾斜的虚线。

又因为俯视图是上面那样的图，所以还需要在DC中点和D'C'中点连线上任取一点，才会出现俯视图中左上倾斜实线。

两个中位线的交点，只有是DC的中点E了。

连接EC'的话，看到的是符合题意的虚线。

如图所示三棱锥C'-AEC就是我们要找的三视图对应的原几何体。

-----------------------------------------------------------------------------------------------------

上面的三视图题目难度算是比较大的了，下面这个题目难度更大。

根据三视图的各个顶点，我们仍然可以判断出来，几何体是从正方体里面截取出来的。

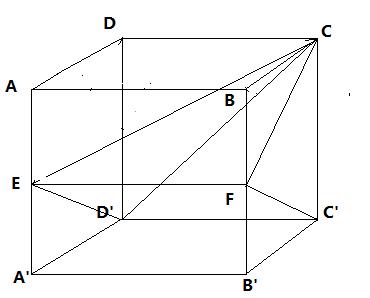
接下来我们一点点地来分析，看看怎么从正方体中截出来三视图是题目中那样的几何体。

首先，俯视图是个正方形，说明AA' BB' CC' DD'四条棱要至少各取一个点（可能取多个点）。

根据侧视图，我们首先可以确定AA' 和 BB'棱上必须只取中点才可以。

根据正视图右上角点，CC'棱上要取C点，根据正视图右下角点，CC'棱上也要去C'点。

根据正视图上面的斜线下段点，我们需要从AA'和DD'中点连线上任取一点，才会出现正视图上面倾斜的线。

又因为侧视图是题目中那样的，所以中点连线上只能取AA'的中点E点才行。

再根据正视图内部的虚线，我们需要从AD'上任取一点和C相连，才会出现虚线那种形式。

再根据侧视图是题目中那样的，所以这一点只能取D'这个点。

最终截出来的图形就是C-EFC'D'这个四棱锥。

知道了几何体是什么样的，再求外接圆表面积还是有很大难度，在这里先不说了，后面会有专门的外接圆内切圆专题解析。

-----------------------------------------------------------------------------------------------------------

上面的题目如果能够搞得懂，可以再试试下面的这个题目，难度也是一样的。