小波分析 原理（小波分析既见森林）

今天看到了一篇不错的文章，来源于创新研究公众号，感谢译者，特此和大家分享一下。

1996年到2003年，美国国家科学院识别和追踪了一些重要技术进步和医学进步的起源，并开展了一系列案例研究。这些案例研究揭示了基础科学所扮演的关键角色，展示了基础研究如何从实验宜或偶然的发现中逐渐发展为可应用于实践的技术，甚至进一步商业化和产业化，成为服务于社会、造福于人类的产品。实际上，科学家们最初在开展这些基础研究时，并无法预测到其实际应用，但恰恰正是这种自由探索式的基础研究，最后催生了诸如人造皮肤、昆虫信息素、人工耳蜗、人类基因检测等技术或产品，本次讲小波分析。

1998年11月15日，华特迪士尼影音公司（Walt Disney Pictures）与皮克斯动画工作室（Pixar Animation Studios）共同发布了一部全电脑动画电影，名为《虫虫危机》（A Bug's Life）。对这两家公司而言，这样的合作已经是第二次了。正如三年前第一次合作的《玩具总动员》（Toy Story）取得的开创性成绩一样，影片《虫虫危机》也获得了一片褒评之声。一位评论家说：“《虫虫危机》充满美妙的视觉创新；其中错综复杂的细节，令大人与小孩都从始至终眼神不离；而影片蕴含的色彩，取自于某种新奇的、至今难解的配色方案……”

只有最懂电脑图形学且常看电影的人，才会思考使用数学建模技术，以动画的形式展现出故事中的种种形象,比如蚂蚁们繁杂的肌理、丰富的表情，各种跳跃、振翅和“嗡嗡”作响的样子。然而，正如人们所见，有一种建模技术在这部电影中首度得到使用。该电脑动画方法运用了一系列数学程序，我们称之为“小波”。

对于小波，一种理解方法是考虑我们的眼睛看待世界的方式。在现实世界中，你可以从多个视角观察一片森林，而实际上，不同的视角就是不同的分辨率。比如，从一架飞过乡村的喷气式飞机的窗口看去，森林就像是一顶连绵的绿色华盖；从一辆行驶在陆地上的汽车的窗口看去，你看到的就是一棵棵独立的树；如果你停下车来近距离地去看，你就会看到树枝和树叶；而如果你在这时掏出一个放大镜，你可能又会发现一片叶子上发现挂着一颗露珠。随着你的镜头不断地拉近、再拉近，你会发现前所未见的细节。但若是对着一张照片重复刚才的做法，你就会对结果感到失望。因为通过放大照片来“近距离”地看这张照片的一颗树，你只能看到一棵更模糊的树，而无法看到树枝、树叶以及叶子上的露珠。尽管我们的眼睛能在不同分辨率下看到森林，但是照相机一次只能呈现出一种。

电脑并不比照相机做得更好。事实上，电脑的分辨率级别是很低的。展示在电脑屏幕上，图片就变成了一个像素集合体，远比不上原始图像那般清晰。

然而，用不了多长时间，电脑就将能做到一直以来摄影师梦想中的事情。电脑将能展示出森林的交互式图像，其中，观者能通过拉伸看到树木、树枝甚至树叶的更多细节。而之所以能实现这一点，是因为小波使得图像数据压缩成为可能，只需更少的空间就可以存储细节更为详尽的图像。

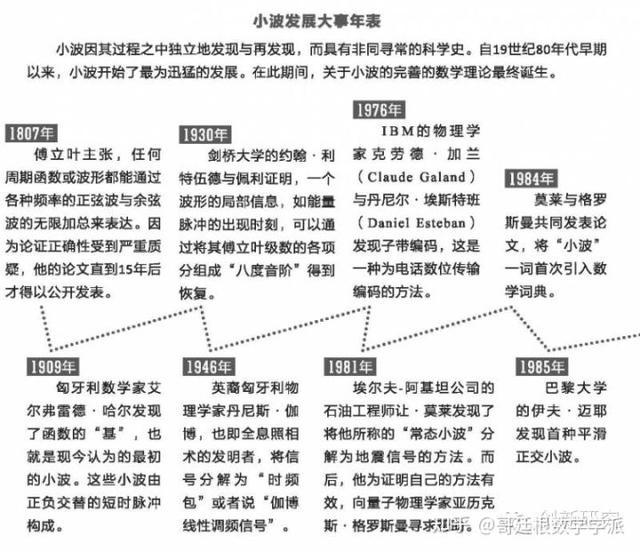
作为一个系统化的研究课题，小波的历史还不到二十年，尽管如此，它却是产生于繁星般众多的相关思想之中，而这些思想已经经历了近两个世纪的发展；在不同学科领域的科学家解决技术问题的过程中，这些思想也不断地被再次发现。信号处理者寻求通过电话线路清晰地传递信息；石油勘探者则需要能够更好地解译地震记录道。然而，“小波”成为科学家中家喻户晓的词却是在从种种应用—也即其产生的源头中抽离出来，综合为一个纯数学理论之后。反过来，综合的结果也开阔了科学家的视野，促进了新应用的产生。举例来说，如今，小波不仅应用于电脑成像与动画制作，而且也被美国联邦调查局（FBI）用来对三百万的指纹数据进行编码。将来，科学家还会利用小波分析来诊断乳腺癌、发现心脏异常与预测天气。

一、改变现实

小波分析使得研究者能够抽离与改造隐藏在繁杂数据之中的特殊模式类型，而这与我们通过眼睛在一片森林中挑出目标树木，或者通过耳朵在一部交响乐中分辨出笛声的原理大致相同。要理解小波的工作原理，我们可以从一种方法开始：找出两种声音的不同点—比如音叉和人声。敲击音叉，你会听到一种持续很长时间的纯音。数学理论称这种音调的频率是“局部化”的，也就是说，它由单音组成，不存在更高频率的泛音。相比之下，人所说的每一个字仅仅持续一秒钟，因此可认为其在时间上是局部化的。其之所以不是频率局部化，是因为说出的字并非单音，而是许多不同频率的组合。

音叉与人声产生的声波图像突出了两者的不同之处。音叉的振动轨迹是数学家口中的正弦波—一个平滑的波状曲线，理论上来讲将一直重复下去。相反，“多脂（greasy）”的图像却包含了一系列尖锐的波峰，没有任何来回振动的迹象。

19世纪，数学家完善了一个可称之为现实的 “音叉”版理论，也就是我们所知的傅立叶分析。法国数学家傅立叶（Jean Baptiste Joseph Fourier）在1807年提出，任何重复波形（或者周期函数），如音叉的声波，都能由各种频率的正弦波与余弦波的无限加和来表示。

傅立叶理论的一个常见阐释见于音乐之中。音乐家演奏一个音符，便创造了一个形状不规则的声波。而只要持续演奏该音符，同样形状的波就会不断重复。因此，根据傅立叶的学说，该音符可以被分解成多个正弦波与余弦波之和。频率最低的波称为该音符的基频，频率更高的波称为泛音。比如，在小提琴或长笛上演奏音符A，就会得到每秒周期为440的基频以及频率为880、1320等的泛音。即使使用小提琴和长笛演奏同一音符，它们听起来也会不同，因为它们的泛音有着不同的强度或“振幅”。正如20世纪60年代的音乐合成器所展示的那样，通过将适当振幅的纯正弦波重新组合，可以逼真地模拟出小提琴或长笛的乐音。当然，这正是1807年的傅立叶所预计的。

后来，数学家将傅立叶的思想扩展到非周期函数（或波形），这种函数的形态会随着时间发生改变，而不是永远重复下去。最接近现实世界的波是这样的：如一辆摩托车加速、减速，且不时熄火所发出的声音。在图像中也是如此，重复与非重复模式之间的区别很是重要。重复的模式可以被视作纹理或背景，而非重复的模式将会作为目标由眼睛挑选出来。周期性或重复的波由一系列离散的泛音组成，它们能被用于展现一幅图像中重复的模式（如背景）。非周期的特性可以被分解为一种更为复杂的频率谱，称为“傅立叶变换”，这就如同太阳光能被分解成由不同颜色构成的光谱一样。相对于传统的波形图，傅立叶变换以更具揭示性也更为集中的形式刻画了周期性波的结构。举例来说，在傅立叶变换中，摩托车发出的“嘎嘎”声将表现为在某个频率上出现峰值。

傅立叶变换曾经是一项重大的成就。在19世纪，它解决了物理学与工程学的诸多问题。它的显著与卓越使得科学家与工程师将它作为分析任何现象的首选方法，而它的无所不在也迫使人们对其进行更为深入的检验与考查。结果在20世纪，数学家、物理学家与工程师意识到了傅立叶变换的一个缺陷：在重塑瞬时信号或是骤变信号时，比如说出的话语或是小军鼓的敲击声，使用该方法存在困难。音乐合成器尽管很不错，却仍然不能与音乐厅小提琴家的演奏相契合，因为小提琴家的演奏有着瞬时的特性，如弓与弦的接触，这很难使用正弦波模拟出来。

这一问题所隐含的原理能够用著名的海森堡测不准原理来说明。1927年，物理学家海森堡（Werner Heisenberg）指出，即使从理论上来讲，一个物体的位置和速度也不能同时得到精确的测量。在信号处理的领域，这就意味着同时知晓精确的频率与该频率在信号中的精确发生时刻是不可能的事情。为了知道其频率，信号必须在时间上展开，反之亦然。在音乐的领域，所谓取舍就意味着任何短时间的信号必然有一个由多种多样的正弦波组成的复杂频谱；反过来，任何由一些正弦波简单合成的信号在时域中必然表现得足够复杂。因此，我们不能期待仅由音叉构成的管弦乐能够重塑击鼓的声音。

二、一个无名者的思想

整个20世纪，不同领域的科学家都在努力挣脱这些限制，目的是使得数据的展现与信息的天然特性相适应。从本质上来讲，他们既想捕捉低分辨率下的森林，即重复的背景信号，也想捕捉高分辨率下的树木，即背景中个别的、局部的变动。尽管科学家都试图在自己的研究领域中解决这个问题，但他们却渐渐得出了一个相同的结论——那就是，问题在于傅立叶变换自身。而实际上，他们也采用了相同的解决方法，即把信号分割成一个个非纯正弦波的组块，如此一来，同时在时域和频域压缩信息成为了可能。这就是后来被称为小波的思想。

第一个参与小波研究的是匈牙利数学家艾尔弗雷德·哈尔（Alfred Haar），他在1909年提出了现在被称为哈尔小波的函数。这种函数仅仅由短时正负交替的脉冲组成。尽管在讲授小波理论时，哈尔小波的短时脉冲表现得十分出色，但对于大多数应用来说，它却没那么实用，因为它描绘出的是锯齿状线而非平滑的曲线。举例来说，哈尔小波重构出的图像看起来就像是一个廉价的计算器屏所显示的那样，而其重构出的长笛声也太过刺耳。

在接下来的几十年里，其他的小波理论先驱者先后出现。20世纪30年代，英国数学家里特伍德（John Littlewood）和佩利（R.E.A.C Paley）开发出了一种根据八度音阶为频率分组的方法，从而创造出了频率良好局部化的信号（其频谱在一个八度音阶以内），而且在时间上也能相对好地局部化。1946年，英裔匈牙利物理学家丹尼斯·伽柏（Dennis Gabor）提出了伽柏变换。类似于傅立叶变换，它把一个波分割成“时频包”或者“相干态”，最大可能地在时间和频率上同时局部化。20世纪70年代和80年代，信号处理界和图像处理界提出了他们自己的小波分析版本，为其命名为“子带编码”、“正交镜像滤波器”和“金字塔算法”。

虽然并非完全相同，但所有这些技术都有着相似的特性。它们把信号分解或转换成组块，这些块能以任何时间间隔实现局部化，也能通过拉伸或压缩从而在不同分辨率下对信号进行分析。此外，小波的先驱者们还有一个共同点：所有人对小波在自己专业外领域的应用都不了解。直到1984年，系统化的小波理论才最终产生。

三、伟大的综合

让·莫莱（Jean Morlet）未曾打算开启一场科学革命，他仅仅是试图为地质学家提供一个更好的石油勘探方法。

通常，石油地质学家通过制造巨响来定位地下油田。因为声波经过不同的物质，其传输速度是不一样的，所以，通过向大地传送地震波并测量其反弹回地表的快慢，地质学家就能够推断出地表之下存在着何种物质。如果这种波能以极快的传播速度穿过某层，那么该层可能会是能够隔离石油的盐丘，石油也许就贮藏在其下方。

理解返回的声波如何反映地下的地质情况（反之亦然），是一个微妙的数学问题。而在习惯上，工程师会使用傅立叶分析来解决该问题。不巧的是，地震信号含有许多瞬变现象——当从一个岩层传播到另一岩层时，地震波会发生骤变。这些瞬变信号恰好包含有地质学家所寻找的信息，也就是岩层的所处位置，但傅立叶分析却会将空间信息分散到整个探测区域。

埃尔夫—阿基坦（Elf-Aquitaine）公司的工程师莫莱开发了他自己的地震信号分析方法，凭此将能生成仅存于局部空间的函数，他称之为“常态小波”。而在日后，人们称之为“莫莱小波”。不论这些函数在时域里如何被拉伸、压缩或移位，它们都能保持相同的形态。而通过在时域内对另一种不同形状的函数（称为母小波）进行拉伸、压缩、移位，就可以塑造出其他小波家族。研究者会发现，母小波的具体形态强烈地影响着近似的准确度和压缩性能。小波的早期版本之间的许多不同之处都可简单地归结为选用了不同的母小波。

莫莱的方法在当时的书中没有，但似乎颇有成效。在他的个人电脑上，他能将一个波分离成多个小波组块，而后又能将它们重新组合成原始的波。但他不满足于经验证据，于是开始询问其他科学家这种方法是否存在数学依据。

亚历克斯·格罗斯曼（Alex Grossmann）是法国马赛的理论物理中心的一位物理学家，莫莱从他那里找到了自己想要的答案。格罗斯曼与莫莱共同工作了一年，为的是证实波能够从自身的小波分解中得到重构。事实上，小波变换反而比傅立叶变换做得更好，因为它对计算中的微小误差不那么敏感。对于傅立叶系数来说，丝毫的误差或是轻率的截断处理就会将一个平滑的信号转变成跳跃的信号，反之亦然，而小波却可以避免这类灾难性的后果。

莫莱与格罗斯曼于1984年发表的论文首次使用了“小波”一词。作为小波理论的奠基者之一而广为人知的伊夫·迈耶（Yves Meyer）当时任职于巴黎的卡尚高等师范学校（ÉcoleNormaleSupérieure de Cachan），他在这年秋天听说了二人的研究，也第一个意识到了莫莱小波与早期的数学小波（譬如利特伍德与佩利的研究所述）之间的联系。（的确，经迈耶计数，在莫莱与格罗斯曼的论文发表之前，互不关联的小波思想再发现已达16个。）

迈耶继续探索出了一种新小波，其具有数学上的正交性，这使得小波变换的操作与运用像傅立叶变换一般容易。（所谓“正交性”，就是一个小波所捕捉到的信息完全独立于另一个小波所捕捉到的信息。）而或许更重要的是，他成为了小波学界融合的纽带。

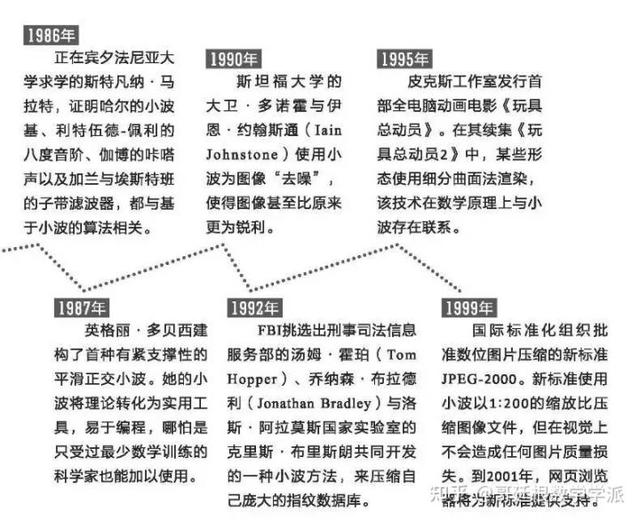
1986年，迈耶的一位以前的学生，当时正在攻读计算机视觉博士学位的斯特凡纳·马拉特（StéphaneMallat），将小波理论与已存在的关于子带编码和正交镜像滤波器的著作结合起来，也就形成了图像处理界的小波版本。多分辨率分析的思想——也就是在不同尺度的分辨率下观看信号——对于图像处理专家来说当时已很熟悉。通过与迈耶的合作，马拉特证明了小波是隐藏在多分辨率分析过程之中的。

得益于马拉特的研究，小波变得更加易于上手。如今，在不知道母小波表达式的情况下，人们就能够做小波分析。分析过程也更为简化：只需将多个像素组取平均，而后得出组间差，如此重复下去即可。对于被“滤波器”、“高频”、“低频”这些熟悉词汇所环绕的电子工程师来说，小波的语言也变得更为得心应手。

小波革命最后一次伟大的进步出现于1987年。对纽约大学库兰特研究院（Courant Instituteat New York University）的访问以及后来在AT&T贝尔实验室的任职使得英格丽·多贝西（Ingricd Daubechies）发现了一类全新的小波，它们不仅正交（与迈耶的小波相同），而且能用简单的数字滤波的思想来实现（事实上，使用长度较短的数字滤波器）。这类新小波的编程与使用几乎与哈尔小波一样容易，但是它却很平滑，没有哈尔小波那般的跳跃。如今，信号处理者有了理想的工具：一种能够将数字数据拆解成多种尺度的组成部分的方法。将多贝西与马拉特的思想结合起来，就有了一个简单的、使用现代计算机能够进行快速计算的正交变换。

多贝西小波有着出乎意料的特性，比如与分形理论间具有紧密的联系。观看其放大后的波形，不论倍数如何，都能看到特有的锯齿形摆动。细节中精致的复杂性意味着，这些小波并不存在简单的表达式。它们是笨拙而又不对称的，面对它们，19世纪的数学家会因恐惧与厌恶而退却。但像福特T型车一般，它们又因实用而美丽。多贝西小波编程起来十分容易，从而实现了从理论到实用工具的转换，哪怕是具有少量数学基础的科学家也能加以使用。

四、小波是怎样工作的？

截至目前，在数字图像压缩方面的应用是小波“最招人喜爱的应用”。在新JPEG-2000数字图像标准以及WSQ方法（小波标量量化方法，FBI用其压缩指纹数据库）之中，小波都处于核心地位。就此而论，我们可以将小波视作图像的建筑基石。使用最宽的小波可以制作出一幅森林的图像：一长条绿色代表森林，一抹蓝色代表天空。若想看到更多的细节，锐度较高的小波能够帮助我们在树与树之间进行区分；而更加精细的小波可将树枝与针叶也添加到图像中。如同绘画中的单个笔触一样，每个小波自身并非图像，但是众多小波集结在一起就能重现任何东西。而不同于绘画中单个笔触的是，小波能被设置成任意的小：单个小波没有物理尺寸的限制，因为在电脑的内存中，它简单地以一系列0和1的形式存储。

与普遍的看法相反，小波自身并不会压缩图像：其作用是使压缩成为可能。要理解其中原因，先假设一幅图像被编码为一系列空间编排数字，比如1，3，7，9，8，8，6，2。如果每个数字对应一个像素的明暗度，0表示白色，15表示黑色，则该字符串代表着某一明亮背景（1，2，3）之上的灰色对象（7，8，9）。

最简单的多分辨率分析通过对每对相邻像素取平均来对图像滤波。在上文的例子中，这一操作得到的字符串结果是2，8，8，4：分辨率稍低，但表现的仍是某一明亮背景之上的灰度对象。如果我们想要由此重构原始图像的降质版本，那么我们可以对字符串中的每个数字进行复制，得到：2，2，8，8，8，8，4，4。

然而，若我们希望完美地退回到原始图像，那么在进行第一步处理时我们应该保存某些附加信息，也就是一些数字集，通过对低分辨率信号进行加或减该数字集即可得到高分辨率信号。在这个例子中，我们所需的数字是-1，-1，0，2。（例如：将第一个像素2加上-1，则会得到1，也就是原始图像的第一个像素；将2减去-1，则会得到3，也就是原始像素的第二个像素。）

因此，在第一步，多分辨率分析将原始信号分割成一个低分辨率部分（2，8，8，4）和一个高分辨率部分，或称“细节”部分（-1，-1，0，2）。高频细节也称为哈尔小波系数。事实上，这整个过程就是哈尔于1909年发现的小波变换的多分辨率版本。

看上去，小波变换的第一步似乎并没有取得任何成果。原始信号中有8个数字，变换后的信号中仍然有8个数字。但在标准的数字图像中，大部分像素与它们的相邻像素都非常相似：天空的像素点会互相毗邻，森林的像素点也会互相毗邻。而这意味着，邻近像素的平均值会与原始像素几乎相同。如此一来，大多细节系数会是0，或是非常接近0。如果我们简单地将这些系数近似为0，那么我们仅需保留的信息就是低分辨率图像以及少数未被近似为0的细节系数。从而，存储图像所需的数据量已被压缩了将近一半。将高精度数字近似为具有更少数位的较低精度数字的过程称为量化（即“小波标量量化”中的“量化”）。

变换与量化的过程想重复多少次都可以，在每次处理过程中，数据量几近减少了一半，图像的质量却只会稍稍降低。根据用户的需求，该过程可在分辨率开始明显变低前停止；或者也可以继续下去，得到指甲盖大小的极低分辨率图像和更加精确的细节图层。有了JPEG-2000标准，即使缩放比达到200：1，也感觉不到图像质量的差别。该小波分解一次对多个（超过两个）邻近像素取平均得到。例如，最简单的多贝西小波变换以4个像素为一组进行组合，而更光滑的变换采用6个、8个甚至更多个为一组的组合方式。

小波有一个令人着迷的特性，那就是它们自动挑选出的特征与人眼的选择相同。量化后存留下来的小波系数对应于与相邻像素差异比较大的那些像素——比如图像中物体的边缘。因此，小波主要通过描画边缘来重现图像，而这与人们素描时的做法恰恰相同。的确，一些研究者指出小波变换与人类视觉的类似并非偶然，因为我们的神经细胞过滤视觉信号的方式与小波相似。

五、将来的小波

伴随小波理论根基的牢固，这一领域在过去十年有了飞速的发展。1990年，关于小波研究刊物的订阅者仅有40人，如今小波研究已拥有了在线的新闻通讯，有着超过17000名的订阅者。此外，通过理论与实践的良好结合，小波一直处于发展之中。工程师总是不断地尝试新的应用，而对数学家来说，仍有重要的理论问题亟待解答。

尽管小波以图像压缩而闻名，但许多研究者也有志于将小波用于模式识别。比如，在预报天气方面，它们可以对带来冗杂数据的现行电脑模型进行瘦身。传统上来讲，这类模型会在大量网格点上对气压进行采样，而后利用样本信息预测数据的演化。然而，这种方法占用了大量的电脑内存。一个使用1000×1000×1000网格的大气模型需要十亿数据点，而这仍然是一个十分粗糙的模型。

另一方面，网格中的大多数数据都是冗余的。你所在城镇的大气压很可能与一英里外的大气压近乎相同。如果将小波应用于天气模型之中，那么在考虑数据时，这些模型将采用与天气预报员相同的方式，重点关注发生骤变的地方——即暖锋、冷锋等。流体力学的其他问题也都能以相同的方法得到解决。例如，洛斯·阿拉莫斯国家实验室（Los Alamos National Laboratory）将小波用于研究炸弹爆炸所产生的冲击波。

正如近期上映的一连串全电脑动画电影所展示的那样，小波在电影产业也有着明媚的未来。这是因为小波变换是一个可逆过程，故合成图像（用小波来建构图像）与分析图像（将图像分解为小波组块）一样容易。这一思想与一种名为细分曲面的新电脑动画方法有关，主要就是多分辨率分析的逆操作。要描画一个卡通形象，动画绘制者只需确定一些关键点，为其创建一个低分辨率版本即可。之后，电脑就可以做逆多分辨率分析，使得形象看起来像真人一般，而不再是一个呆板的图画。

细分曲面在1998年的电影《虫虫危机》中首度采用，取代了稍显笨拙的NURBs（非均匀有理B样条曲线）方法，而NURBs曾于1995年在《玩具总动员1》中应用过。有趣的是，1999年的《玩具总动员2》同时使用了这两种方法，曾于《玩具总动员1》中出现过的人物依旧使用NURBs，而新人物则是基于细分曲面法。细分曲面法的下一个应用领域或许会是视频游戏产业，在这一产业中，细分曲面法可能可以消除目前的制图法的块状外观。

与此同时，在理论方面，数学家仍然在为二维和三维图像寻找更好的小波种类。标准的小波方法虽然善于挑拣边缘，但一次却只能处理一个像素——对于展现极为简单的曲线或线条而言，这太过低效。斯坦福大学的大卫·多诺霍（David Donoho）与伊曼纽尔·康代（Emmanuel Candès）提出一类名为“脊波”的新式小波，其经过特别设计能够检测直线上的不连续部分。其他研究者则在研究“多小波”，其可以用来编码在同一路线上传输的多重信号，如彩色图像，每个像素的三种颜色值（红、绿、蓝）必须一次性传送。

当被要求证明数学的价值时，数学家们常常会说，为解决一个纯粹数学问题而发展出的理念在若干年后会有意想不到的应用。但是小波的故事描绘出了一幅更为复杂也颇为有趣的图景。在其中，特定的应用研究引发了新的理论综合的产生，而新的理论综合反过来也开拓了科学家开展新应用的视野。也许，小波给予我们的更多经验教训是，不要将基础科学与应用科学的努力割裂来看：好的科学要求我们既看到理论上的森林，也看到实践中的树木。

,