高一数学函数的最大值最小值（高一数学第一次月考考点之函数最大值和最小值详解）

Hello，这里是摆渡学涯。

这次课程我们来为大家讲一下月考中必考的内容之函数的最大值和最小值的求解技巧，教你轻松应对第一次的月考。

最大值：经常表示为max，最大值表示函数在给定区间内的最大的值，即任意的函数值都要小于这个函数值。

最小值：经常表示为min，最小值表示函数在给定区间内的最小的值，即任意的函数值都要大于这个函数值。

如函数f（x）=2 x 4，在（2，3）上单调递增，f（2）为f（x）的最小值，f（3）为f（x）的最大值。

答案是否定的，在给定的区间上，不是所有的函数都有最大值和最小值的，要根据实际情况进行实际分析的。如一次函数，f（x）=2 x 4在定义域R上的值域也是R，即这个时候是没有确定的最大值和最小值的，最大值为正无穷，最小值为负无穷，但是正无穷和负无穷都不是一个固定的数值哦。

二次函数有没有最大值和最小值和函数的定义域有很大的关系。如：二次函数f（x）=ax的平方 bx c中（a不为0），当a>0时，函数的图像开口向上，在定义域R上函数有最小值，最小值为f（-b/2 a），当a<0时，函数的图像开口向上，在定义域R上函数有最大值，最大值为f（-b/2 a）。

当指定二次函数的定义域时，要看给定的区间是否包含二次函数的对称轴，如果二次函数开口向上，那么距离对称轴越远，函数值会越大，反之，如果二次函数开口向下，那么距离对称轴越远，函数值会越小，直接利用这个结论进行最大值和最小值的求解即可。

这个比较简单，直接利用函数的单调性进行求解即可，此处不再赘述。

当未知函数的表达式时，已知函数的最大值和最小值需要求出函数的表达式，方法比较简单，首先要知道最大值对应的函数表达式和最小值对应的函数表达式，然后联立方程组进行相关的参数求解即可。考点基本上就这些了，下面我们给出详细的题目进行讲解和说明。

例题1：已知f（x）=3 x的平方 4，求f(x)的值域

解：由题意知，二次函数的开口向上，定义域为R，因此函数有最小值，最小值为f(-b/2 a)=f(0)=4，所以f（x）的值域为{f(x)|f(x)>4}。

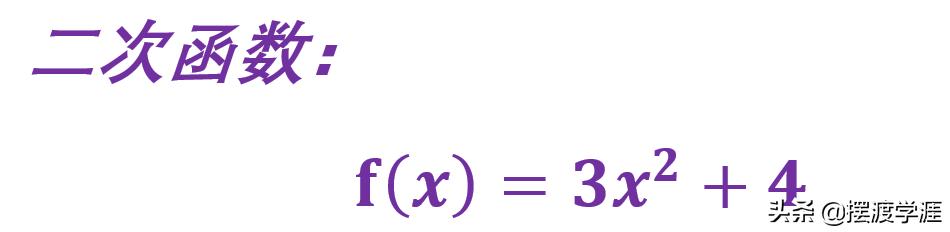
例题2：已知f（x）=3 x的平方 4，求f(x)在[3，4]上的最大值和最小值

解：由题意知，二次函数的开口向上，且定义域[3，4]不包含对称轴x=0，利用二次函数到对称轴的距离越远函数值越大进行求解知：f（3）为函数的最小值，f（4）为函数的最大值，得：f（x）的最大值为52，最小值为31。

例题3：已知f（x）=3 x的平方 4，求f(x)在[-1，1]上的最大值和最小值

解：由题意知，二次函数的开口向上，且定义域[-1，1]包含对称轴x=0，因此函数的最小值为f(0)，再利用二次函数到对称轴的距离越远函数值越大进行求解知：f（1）或者f(-1)为函数的最大值，得：f（x）的最大值为7，最小值为4。

例题4：已知f（x）=k x b，在[1,2]上的最大值为4，最小值为1，求f(x)的表达式

解：由题意知：f(x)为一次函数，k不为0，当k>0时函数的最大值为f(2)，最小值为f(1)，即：f(2)=2 k b=4，f（1）=k b=1，解得：k=3，b=-2。

当k<0时函数的最大值为f(1)，最小值为f(2)，即：f(2)=2 k b=1，f（1）=k b=4，解得：k=-3，b=7。

因此函数的表达式为f(x)=3 x-2或者f(x)=-3 x 7

本次课程我们就为大家分享到这里了，咱们下次课再见！如您还有相关的问题，请在下方留言，咱们将第一时间给以大家满意的答复。

声明：本文为摆渡学涯的原创文章，未经作者同意不得进行相关的转载和复制，翻版必究，请务必尊重他人的劳动成果。