十分钟理解线性代数（趣味线性代数七）

给出一组向量（3，-1，1）和（2，2，-1），我们用它来构建一个方程式组，提取系数矩阵，再画出图形，如下：

让我们带上一点强迫症的情绪去审视它们，有毛病没，老铁？

有，太有了！

方程：有三个未知数，为什么只有两个方程？

矩阵：三列为什么配两行，横竖不能一样长吗？

图形：三维坐标系，怎么只画了两条向量线段？

如果你也有上述自我强迫式的疑问，那恭喜你，你的线性代数，要有“秩”的飞跃了。

注意两件事：

1、齐次线性方程组的几何含义是，画出给定的两条向量线段的垂直线段（或直线）；

2、原点（0，0，0）与任意一条向量线段垂直。

那么，在求解之前，关于方程组、矩阵和图形的完整表述应该是这样的：

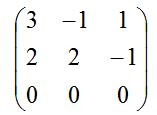
从图形可以看出，与两条向量线段垂直的是一条直线，那么，可以取任意值。试取，得。用解向量（）替代零向量（0，0，0），代入矩阵和图形中，如下图：

从图形的角度看，求解齐次线性方程组也是在测度向量空间。如果向量空间是饱满的，则方程无解；如果向量空间不够饱满，则方程有解，并且解向量正好将它填充。

那么，在不求解的情况下，如何测度向量空间呢？分析一下系数矩阵就可以了，而分析的结果就是矩阵或向量组的“秩”。

给出“秩”的定义：

矩阵的秩：设在矩阵中有一个不等于的阶子式，且所有阶子式（如果存在的话）全等于0，那么称为矩阵的最高阶非零子式，数称为矩阵的秩，记作，并规定零矩阵的秩为。

向量组的秩：设的向量组，如果

（1）、在中有个向量线性无关；

（2）、中任意个向量（如果中有个向量的话）都线性相关，那么称是向量组的一个最大线性无关向量组，简称最大无关组；数称为向量组的秩，并规定只含零的向量组的秩为。

对于阶子式，我们可以把它理解为对N维空间的解构， 以三维空间为例，二维平面和一维直线便是三维空间的“阶子式”。基于有线才有面、有面才体的常识，判定N维向量空间的饱满程度（即矩阵或向量组的秩），可以从二维平面是否有面积（即二阶子式是否为0）开始。

试想一下，常见的三维体都有几个面？长方体有六个面，三棱柱有五个面，三棱锥有四个面。所以，某个二维平面面积为0（即阶子式为0），并不影响三维体的体积，只要找一个面积不为0的二维平面（即阶子式），再由低阶向高阶推演，就可以算来矩阵或向量组的秩了。

比如，上面列出的矩阵：

如果将列向量看作是向量线段，那么向量空间是2维的，2维平面有三条向量线段，两条即可成面，所以，这个矩阵则是满秩的，秩为2，也就是维度数。

如果将横向量看作向量线段，只需要增加一个零量（0，0，0），即

三维的向量空间里，只有两条向量线段，任一个二阶子式不为零，就意味着两条向量线段不共线。而三阶子式（即矩阵本身）是0，意味着这个矩阵对应的是一个二维平面，它的秩为2，而向量空间的维度数是3。

总之，矩阵的“秩”与齐次线性方程组的解、向量组的线性相关和线性无关、向量空间的饱满度，在内在含义上是相通的。