常见物质转化图解(孕育着令人惊叹的副产物)
数学难题的魅力不在于答案,而在于解法。 有些问题可能在解到最后才发现没有答案,虽然这听起来很沮丧,但是整个思维过程却总是伴 随着最美好、最让人兴奋的新发现,你往往能得出一些新的原理。
用直尺与圆规当然可以做出许多种之图形,但有些图形如正七边形、正九边形就做不出来。有些问题看起来好像很简单,但真正做出来却很困难,这些难题之中就有化圆为方的问题。由此产生的一些新思路、新方法和由此派生出的名题,其意义恐怕超过了难题的解决。

1.化圆为方问题,本质上就是要求作 π 的平方根
化圆为方问题(problem of quadrature of circle)是二千四百多年前古希腊人提出的三大几何作图问题之一,即求作一个正方形,使其面积等于已知圆的面积。其难度在于作图使用工具的限制。古希腊人要求几何作图只许使用直尺(没有刻度,只能作直线的尺)和圆规。最早研究这问题的是安纳萨戈拉斯,他因"不敬神"的罪名被捕入狱,在狱中潜心研究化圆为方问题,可惜他的结果失传了。以后著名的研究者更有希波克拉底、安提丰 、希皮亚斯等人。 在中国,尺规作图可以追溯到春秋战国时期,那时候的人们运用尺规参与地图,器械的制造。
尺作图问题曾吸引许多人研究,但无一成功。化圆为方问题,实际上就是用直尺圆规作出线段π的问题。1882年法国数学家林德曼(1852-1939)证明了π是超越数,同时证明了圆为方问题是标尺作图不可能的问题。因为十九世纪有人证明了若设任意给定长度单位,则标尺可作的线段长必为代数数 。而化圆为方问题相当于求作长为√π的线段,但√π并非代数数,故此标尺不可作。
几千年前,数学家们就接近化圆为方来,但是这些早期的所作都基本于一个假设,那就是π能够表示为两个整数的比值。现在人们不仅知道π是无理数,而且在19世纪的时候就已经证明了它是超越数。几个世纪以前,数学家们已经相互独立的证明了超越数不可能由直尺和圆规构造出来,明确地解决了这个问题。
尺规作图只能进行四则运算和开平方,对作为超越数的 π 无能为力。但这并不能阻挡某些"数学爱好者"的脚步。
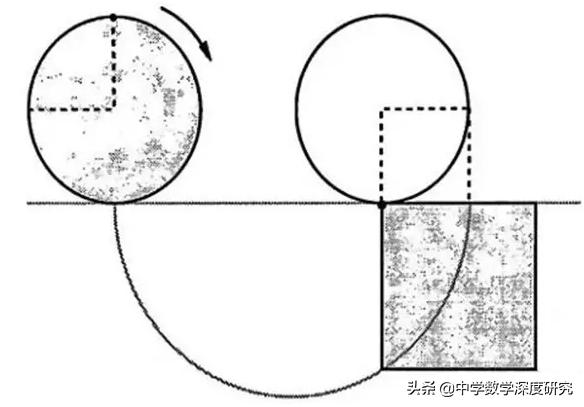
二千年间,尽管对化圆为方问题上的研究没有成功,但却发现了一些特殊曲线。希腊安提芬(公元前430)为解决此问题而提出的"穷竭法",是近代极限论的雏形。大意是指先作圆内接正方形(或正6边形),然后每次将边数加倍,得内接8、16、32、…边形,他相信"最后"的正多边形必与圆周重合,这样就可以化圆为方了。虽然结论是错误的,但却提供了求圆面积的近似方法,成为阿基米德计算圆周率方法的先导,与中国刘徽的割圆术不谋而合,对穷竭法等科学方法的建立产生直接影响。

值得关注的是,穷竭法由古希腊的安提芬(Antiphon)(公元前430)最早提出,后来,古希腊数学家欧多克斯(Eudoxus of Cnidus)做了改进,将其定义为:在一个量中减去比其一半还大的量,不断重复这个过程,可以使剩下的量变得任意小。阿基米德进一步改进这种方法后,将其应用到对曲线、曲面以及不规则体的体积的研究和讨论上,为现代积分学打开了一道隐隐的门。由于涉及到超越数(transcendentalnumber)π,传统的尺规作图和折纸作图必定无法解决,持续了上千年的争论终于尘埃落定。所以如果真要解决这一问题,我们需要借助更加"先进"的阿基米德螺线才行了。

这个精力旺盛而长寿的天才还通过使用圆外接正多边形和圆内接正多边形逼近圆周率的真实值,他最终使用到了九十六边形(因为 96 = 2 5 * 3 ,稍后我们会发现这个多边形正巧是可以通过尺规作图做出来的),得到π的真实值在 3.14163 和 3.14286 之间。
2. 利用密率,近似作图很精巧
化圆为方难题本质体现了用尺规作图是作不出π这一长度的,但我们可以用尺规进行作图的是,是用一个与圆周率π非常近似的且分子分母都是正整数的分数来代替圆周率,从而可以用尺规进行作图,作出π的近似长度。这里用来代替圆周率π的分数就是由中国伟大数学家祖冲之最先发现的非常著名的分数——密率:355 / 113。把它表示成小数,它的小数点后6位数字都是正确的:3.141592......,这已经很精确了。
我们先把355 / 113写成下面的形式:

上面这个式子先放在这里,后面我们将会看到,上式最右边那个复杂的分数,竟然可以用尺规作图方法作出来。
我们下面开始作图,完全是尺规进行。作半径为1的半圆ACB。点O为圆心,OC垂直于AB。在OC上取一点D,使OD=7/8。连接AD。在AD上取AE等于1/2。过点E作AB的垂线EF,F为垂足。连接FD,过点E作EG∥FD,点G在AF上。

由△AEF 与 △ADO 相似,得
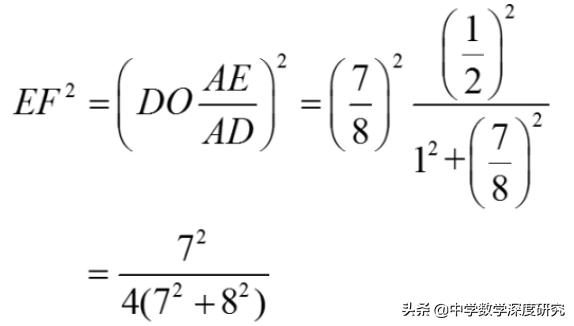
在△AEF中,有


由△AEG与△ADF相似,得

于是,由最前面那个式子:

可以看出,圆周率π的近似值——密率:355/113,可以根据刚才已得到的线段AG加上3个AO的长度,用尺规进行度量。我们可以在一条直线上画出AG 3AO这么长的线段。如下图红线段所示:

如上图所示,再在长度为π的线段的右侧同一直线上接上一条长度为1(也就是AO)的线段。以这两条线段的长度为直线作半圆。过这两条线段的交界点作这两条线段的垂线(图中蓝色),与半圆相交。那么,根据相交弦定理,交点到直径的距离就为√π,我们就以这条垂线段为一边作正方形。那么,这个正方形的面积极为近似地等于π,即等于半径为1的圆的面积。所以,作一个面积等于某圆面积的正方形这一"化圆为方"问题,在用密率近似表示圆周率的情况下,用尺规作图可以解决。
3. 达·芬奇的狡猾"解法"
其实,若不受标尺的限制,化圆为方问题并非难事,欧洲文艺复兴时代的大师芬兰数学
家达芬奇(1552-1519)假设圆半径为 r,造一个半径为 r 高度为 r/2 的圆柱体,它的侧面面积恰好就是 πr 2 。接下来就好办了,用绳子把圆柱体的"腰围"和"身高"量一下,放到纸上形成一个矩形,然后用直尺圆规来将这个矩形化为正方形就好了。这个方法相当狡猾,用"度量"的方法巧妙避开了"作出 π 的平方根"这个问题。

当然,在欧几里德这些希腊人的眼中,这种方法只是取巧,因为一来不精确,二来太犯规,用了直尺圆规以外的工具。即使用直尺和圆规来度量也不行,尺规作图的规定就是,直尺只能拿来画直线,圆规则是画圆,它们不能有"度量"的功能。
4.新观点下的破解之法
(1)塔斯基的问题,数学家塔斯基(Alfred Tarski)在 1925 年提出的,正是这样一个挑战。用更精确的数学语言来说,就是要求把平面上的单位圆盘分割成有限块,每一块是一个点集,然后通过平移和旋转这些保持面积的方法,将这些点集拼成面积相同的正方形。怎么分割都无所谓,甚至是没办法做出来的分割也可以,唯独是"有限块"这种限制不能去掉。如果能分割成无限块的话,那就太简单了,只要把单位圆盘"磨成细末",每一块都只有一个点的话,那别说是拼成正方形,就是拼成一幅对联也问题不大。即使是犯规,也是有底线的。
这乍听起来是个很无理的问题。别的先不说,要把圆变成正方形,总要先处理那弯弯的圆周吧?看起来无论怎么切,只要是有限块,那恐怕也不能将弯曲的边界拗成直线。实际上,可以证明,如果只用剪刀这样的工具的话(从数学上来说就是如果每一块的边界都是简单闭合曲线的话),这个任务是不可能做到的。但是,原来的题目中也没有限制只能用剪刀。只要是"点集",无论是否连在一起,都符合要求,所以希望还有,不过就是更"犯规"一点而已。

(2)拉兹柯维奇的答案,在 1990 年,匈牙利数学家拉兹柯维奇(Miklós Laczkovich)终于肯定地解答了塔斯基的这个问题。他证明了这样的先割后补的"化圆为方"方法是存在的。美中不足的是,他并没有实际给出一个割补的方法,而只是证明了这样的方法存在,而且粗略估计需要将圆切成大约 10 的 50 次方个点集。而更为犯规的是,这些点集是没有面积的。这些点集甚至不是面积为 0,而是我们根本无法定义它们的面积。在数学上,这些无法定义面积的点集叫不可测集。为了定义这些集合,拉兹柯维奇在证明中大量使用了选择公理,这是定义不可测集的唯一方法,也是令我们不能明确构造分割方法的原因。

如果提出尺规作图化圆为方问题的希腊人来到今天,看到这个犯规的割补法竟然与数学推理的基础有着联系,他们会做何感想呢?
虽然三大几何作图难题都被证明是不可能由尺规作图的方式做到的,但是为了解决这些问题,数学家们进行了前赴后继的探索,最后得到了不少新的成果,发现了许多新的方法。同时,它反映了数学作为一门科学,它是一片浩瀚深邃的海洋,仍有许多未知的谜底等待这我们去发现。
,免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。文章投诉邮箱:anhduc.ph@yahoo.com






