高中数学必修一函数的单调性讲解（高中数学必修一）

一：函数单调区间的求法：

（1）图像法

对于能作出图像的函数，我们可以通过观察图像确定函数的单调区间，即第一步作出函数图像，二是由单调性的几何意义划分增减区间，最后一步写出单调区间。

注意：当函数递增或递减区间由几个区间组成时，一般情况下不能取它们的并集，而应该用“和”、“或”连接。

（2）定义法

有些函数如果不能作出函数图像来观察出单调区间，可以用定义法来求其单调区间，即首先可以设X1、X2为该区间内任意的两个值，且X1小于X2，其次作差，令F（X1）-F（X2），并通过因式分解、配方、有理化等方法，向有利于判断差值符号的方向变形。

（3）直接法

对于我们所熟知的一次函数、二次函数、反比例函数等，可以根据它们的特征，直接求出单调区间

（4）复合函数单调性的确定

二：求函数最值的方法

（1）函数的最值

（2）利用函数图像求最值

利用函数图像是函数求最值的常用方法，其步骤如下：

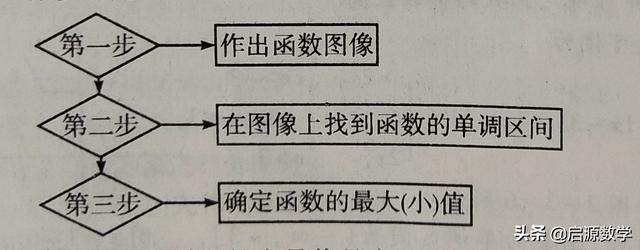
（3）利用函数单调性求最值

函数的最值与单调性的关系：

若函数在区间[a,b]上是减函数，则f(x)在[a,b]上的最大值为f(a),最小值为f(b)；

若函数在区间[a,b]上是增函数，则f(x)在[a,b]上的最大值为f(b),最小值为f(a).