数学k字型模型知识点（再说倍长中线模型）

三角形是初中数学里最基本的几何图形，而其边上中点，又是很常见的条件。当涉及三角形中点或中线问题时，常采用延长中线一倍的办法，即倍长中线法，来作辅助线解题。好处是通过此法构造全等三角形继而得到平行，可将分散的条件集中在一个三角形内解题，常常出奇制胜，化腐朽为神奇。且看模型的探究，和模型产生的基本结论及应用。

[问题提出]

如图1，在△ABC中，若AB＝6，AC＝4，求BC边上的中线AD的取值范围．

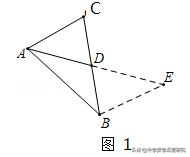
[问题解决]

解决此问题可以用如下方法，延长AD到点E使DE＝AD，再连结BE（或将△ACD绕着点D逆时针装转180°得到△EBD），把AB、AC、2AD集中在△ABE中，可得△DAC≌△DEB得AC＝EB，再根据三角形三边关系求得AE的取值范围，由此得出中线AD的取值范围是　1＜AD＜5.

【模型归纳】

【简单应用】如图2，如图，在△ABC中，D为边BC的中点，已知AB＝5，AC＝3，AD＝2．求BC的长

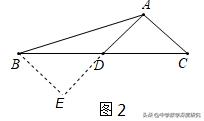
【解析】延长AD到E，使得AD＝DE，连接BE，可证明△DAC≌△DEB得AC＝EB，再证明∠AEB＝90°，由勾股定理求得BD=√13，进而得BC＝2BD＝2√13；

[拓展应用]

如图3，在△ABC中，∠A＝90°，点D是边BC的中点，点E在边AB上，过点D作DF⊥DE交边AC于点F，连结EF，已知BE＝4，CF＝5，则EF的长为____

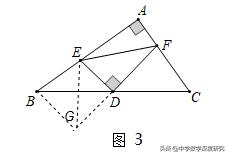
【解析】延长FD到G，使得DG＝FD，连接BG，EG，可证明△CDF≌△BDG，得BG＝CF，∠DCF＝∠DBG，再证明∠EBG＝90°，由勾股定理求得EG=√41，由线段垂直平分线性质得EF=EG=√41，．

【点评】本题考查几何变换综合题、三角形的中线、勾股定理、矩形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，体会出现中点的辅助线的添加方法，属于中考压轴题．由此可归纳如下模型

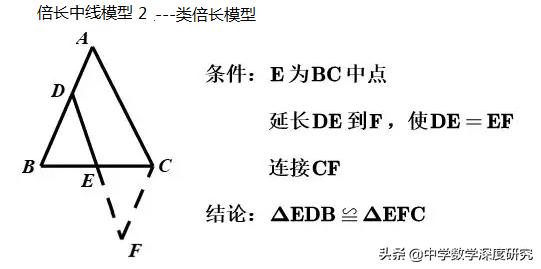
[变式拓展]

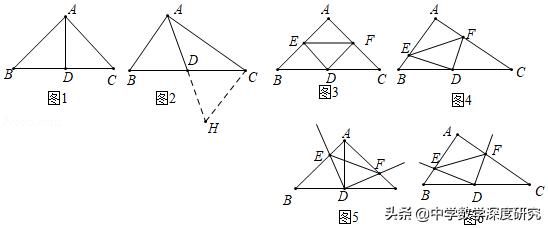
1．（2019春•崇川区校级月考）如图1，Rt△ABC中，∠A＝90°，AB＝AC，点D是BC边的中点连接AD，则易证AD＝BD＝CD，即AD＝1/2BC；如图2，若将题中AB＝AC这个条件删去，此时AD仍然等于1/2BC．

理由如下：延长AD到H，使得AH＝2AD，连接CH，先证得△ABD≌△CHD，此时若能证得△ABC≌△CHA，

即可证得AH＝BC，此时AD＝1/2BC，由此可见倍长过中点的线段是我们三角形证明中常用的方法．

（1）请你先证明△ABC≌△CHA，并用一句话总结题中的结论；

（2）现将图1中△ABC折叠（如图3），点A与点D重合，折痕为EF，此时不难看出△BDE和△CDF都是等腰直角三角形．BE＝DE，CF＝DF．由勾股定理可知DE2 DF2＝EF2，因此BE2 CF2＝EF2，若图2中△ABC也进行这样的折叠（如图4），此时线段BE、CF、EF还有这样的关系式吗？若有，请证明；若没有，请举反例．

（3）在（2）的条件下，将图3中的△DEF绕着点D旋转（如图5），射线DE、DF分别交AB、AC于点E、F，此时（2）中结论还成立吗？请说明理由．图4中的△DEF也这样旋转（如图6），直接写出上面的关系式是否成立．

【解析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可，可得结论：直角三角形斜边上的中线等于斜边的一半．

（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HDC（SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．

（3）图5，图6中，上面的关系式仍然成立．结论：EF²＝BE² CF²．证明方法类似（2）．

【点评】本题属于几何变换综合题，考查了旋转变换，翻折变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．

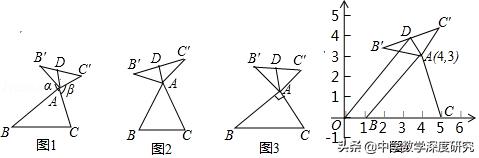
2．（2018秋•吴兴区期末）我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）并缩短一半得到AB'，把AC绕点A逆时针旋转β并缩短一半得到AC'，连接B'C'．当α β＝180°时，我们称△AB'C'是△ABC的"旋半三角形"，△AB'C'边B'C'上的中线AD叫做△ABC的"旋半中线"，点A叫做"旋半中心"．

特例感知：

（1）在图2，图3中，△AB'C'是△ABC的"旋半三角形"，AD是△ABC的"旋半中线"．

①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD＝_____ BC；

②如图3，当∠BAC＝90°，BC＝4时，则AD长为 _____．

猜想论证：

（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．

拓展应用：

（3）如图4，在平面直角坐标系中，△ABC的坐标分别是A（4，3），B（1，0），C（5，0），△AB′C′是△ABC的"旋半三角形"，AD是△ABC的"旋半中线"，连结OD，求OD的最大值是多少？并请直接写出当OD最大时点D的坐标．

【解析】（1）①首先证明△ADB′是含有30°是直角三角形，可得AD＝1/2AB′即可得AD＝1/4BC，；

②首先证明△BAC∽△B′AC′，根据直角三角形斜边中线定理即可解决问题AD=1；

（2）结论：AD＝1/4BC．如图1中，延长AD到M，使得AD＝DM，连接B′M，C′M，首先证明四边形AC′MB′是平行四边形，再证明△BAC∽△AB′M，即可解决问题；

（3）如图4中，先确定OD最大值时，D的位置，D在以A为圆心，以1为半径的圆上，则当D运动到直线OA与半圆相交时OD最大，求此时OD的长并确定其坐标．

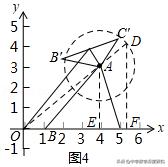
∵A（4，3），∴OA＝5，

∵AD＝1，∴OD的最大值是6．

过A作AE⊥x轴于E，过D作DF⊥x轴于F，

∴AE∥DF，∴△AOE∽△DOF，

∴OA/OD=OE/OF=5/6=AE/DF＝，

∵OE＝4，AE＝3，∴OF＝24/5，DF＝18/5，∴D（24/5，18/5）．

常规的倍长中线可以出全等，但需要证明"三点共线"，遇到"中点 平行"，我们"延长出全等"，而非"倍长出全等". 用"倍长中线法"作辅助线解几何题，是一种重要的技巧套路。它可以有效地生发出全等、平行等基本条件，关联好多基本图形，帮助解题，大家务必好好掌握。也给我们解题的启示：抓住核心，找到关键，才能快速解题。在数学问题的解决过程中伴随着一系列的心智活动，无论进行过程是否顺利，都将给人以启迪和力量。"细雨湿衣看不见，闲花落地听无声。"

像这样在挑战数学典型问题的征途中，经历深入思考、体验，我们的知识、方法、能力、智慧、意志力一定悄然得以提升。

,