高中数学函数值域的11种求法总结（函数值域的常用求解方法）

函数值域是高考数学考点函数的重要性质之一，几乎每年高考都是必考内容，但函数值域确实是部分高中生学习的难点及烦心点。

函数值域的求解，不仅在知识上涉及到高中诸多知识点，除函数的所有知识外，还涉及到二次函数、不等式等其他重要知识点。

函数值域在解题方法上，具有较强的综合性在具体问题中，若能依据函数解析式的特征灵活选择适当的求值域的方法，则可以有效突破函数值域求解这一难点。

本文重点归纳总结求解函数值域的常见方法，以期对高考生学习该部分知识提供帮助。

一、配方法

【点睛】配方法是求二次函数类值域的基本方法，对形如“g(x)=af(x)^2 bf(x) c(a不等于0)”的函数值域问题，均可使用配方法。

二、图像法

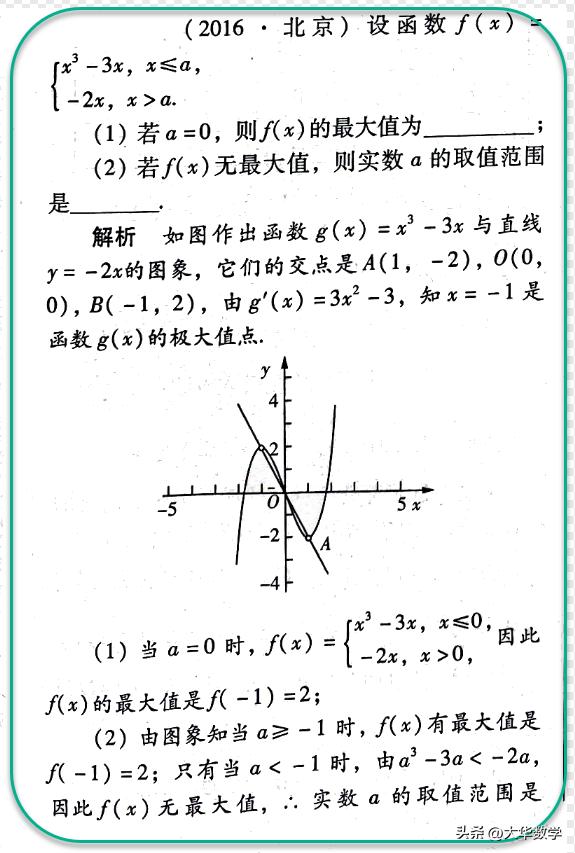
故实数a的取值范围为：a<-1.

【点睛】此法广泛应用于求二次函数在闭区间上的值域和一些分段函数的值域其关键在于能否准确作出函数的图象，利用函数的图象求函数值域，主要体现数形结合的思想是解决许多问题的重要思想。

三、分离常数法

【点睛】对形如“y=(ax b)/(cx d)(a,b,c,d为常数且ac≠0)”的函数，可直接采用分离常数法关键是通过拼凑，将分子进行常数分离。

四、判别式法

【点睛】对形如： 的函数，函数的定义域为 R，则可把函数转化为关于x的一元二次方程，再由，确定y的取值范围，进而求得原函数的值域。

五、换元法

【点睛】常用代数代换或三角代换法，把所给函数代换成值域容易确定的另一函数，从而求得原函数的值域，但换元时要注意新变量的取值范围

六、不等式法

【点睛】借助不等式(a>0,b>0)求函数值域此法要特别注意不等式成立的条件“一正，二定，三相等”。在具体求解过程中，经常进行常数分离。

七、导数法

【点睛】导数法是求解函数值域的通用方法一般用于非函数首先确定函数的定义域，然后再根据导函数在给定的区间上的正负来判断函数的单调性求值域

【总结】求函数值域的方法较多，以上是最常用的几种方法.在具体求函数值域时，需要根据函数的类型特点，灵活运用各种方法进行综合求解。