高中数学第一章计数原理知识点 分类计数原理与分步计数原理

例1、有三个袋子，其中一个袋子装有红色小球20个，每个球上标有1至20中的一个号码，一个袋子装有白色小球15个，每个球上标有1至15中的一个号码，第三个袋子装有黄色小球8个，每个球上标有1至8中的一个号码。

（1）从袋子里任取一个小球，有多少种不同的取法？

（2）从袋子里任取红、白、黄色球各一个，有多少种不同的取法？

解：

（1）任取一个小球的方法可分三类，一类取红球，有20种取法；一类取白球，有15种取法；一类取黄球，有8种取法。由分类计数原理共有20 15 8=43种不同取法。

（2）取三色小球各一个，可分三步完成，先取红球。有20种取法；再取白球，有15种取法；最后取黄球，有8种取法。由分步计数原理，共有

种不同的取法。

例2、在所有的两位数中，个位数字比十位数字大的两位数有多少个？

解：分析个位数字，可分以下几类：

个位是9，则十位可以是1，2，3，……，8中的一个，故有8个；

个位是8，则十位可以是1，2，3，……，7中的一个，故有7个；

与上同样。

个位是7的有6个；

个位是6的有5个；

……

个位是2的只有1个。

由分类计数原理知，满足条件的两位数有

（个）

例3、如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联，连线标注的数字，表示该网线单位时间内可以通过的最大信息量，现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为多少？

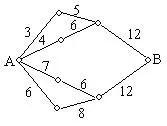
解：沿12—5—3路线传递的信息最大量为3（单位时间内），沿12—6—4路线传递信息的最大量为4……由于以上每个线路均能独立完成这件事（传递信息），故单位时间内传递的最大信息量为3 4 6 6=19。

例4、用6种不同的颜色对下图中5个区域涂色，每个区域涂一种颜色，相邻的区域不能同色，那么共有多少种不同的涂色方法？

解：分五步进行，第一步给5号域涂色有6种方法

第二步给4号涂有5种方法

第三步给1号涂有5种方法

第四步给2号涂有4种方法

第五步给3号涂有4种方法

根据分步计数原理，共有

种不同涂法

例5、求下列各式中的

值

（1）

；（2）

；（3）

。

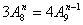
解：（1）由排列数公式，

得

整理得

∴

∴

或

（舍去） ∴

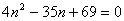
（2）由排列数公式，

得

整理得

解得

或

（舍去） ∴

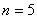
（3）由排列数公式，得

化简得

或

∵

∴

例6、证明下列等式：

（1）

；

（2）

；

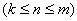
（3）

证明：（1）∵

∴

（2）

（3）∵

∴

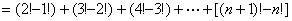
例7、由0，1，2，3，4，5共六个数字可组成多少个没有重复数字且能被5整除的六位数？

解：组成的六位数与顺序有关，但首位不能排0，个位必须排0或5，因此分两类：第一类：个位必须排0，此时前五位数由1，2，3，4，5共五个数字组成，这五个数字的每一个排列对应一个六位数，故此时有

个六位数。第二类：个位数排5，此时为完成这件事（构造出六位数）还应分两步，第一步排首位，有4种排法，第二步排中间四位，有种排法，故第二类共有

种排法，以上两类排法都符合题目要求，所以共可组成

个。

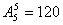
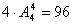
例8、用0，1，2，3，4五个数字组成的无重复数字的五位数中，其依次从小到大的排列。

（1）第49个数是多少？（2）23140是第几个数？

解：（1）1、2是首数时各组成

个不同的五位数，故第49个数是30124。

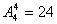
（2）1在万位时有个；2在万位，0、1在千位的共有

个；2在万位，3在千位，0在百位的有

个，还有23104比23140小，故23140是第

（个）数。

例9、四名男生和三名女生按要求站成一排，分别有多少种不同的站法？（1）甲不站在两端；（2）甲、乙二人不能站在两端；（3）甲、乙二人之间间隔两个人；（4）四名男生站在一起，三名女生站在一起；（5）男女互相间隔开；（6）三名女生排列顺序一定。

解：（1）方法一：因为甲不在两端，分两步排队，首先从甲以外的6个人中任选两人站在左、右两端，有

种方法，然后让剩下的5个人（其中包括甲）站在中间的5个位置，有

种方法，因此共有

种站法。

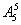
方法二：因为甲不在两端，分两步排队，首先排甲，有

种方法，第二步让其他6人站在其他6个位置上，有

种方法，故有

种站法。

方法三：第一步先让甲以外的人站队，有种方法，第二步让甲插入这6个人之间的空当中，有种，故共有

种站法。

方法四：在排队时，对7个人，不考虑甲的站法要求任意排列，有种方法，但其中包括甲在左端或右端的情况

种方法，因此共有

种站法。

（2）方法一：甲、乙两人为特殊元素，先考虑甲、乙的站法，除两端的其余5个不同位置都可排甲、乙，有

种排法，再考虑其余5个元素的排法有种，根据分步计数原理，甲、乙二人不能站在两端的排法有

种。

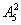
方法二：甲、乙两人不能站在两端，应包括同时不在两端，某一人在两端，故用排异法，应减去两种情况，同时在两端，有

种，某一人在两端，有

种，故有

种不同站法。

（3）分三步：第一步，从甲、乙以外的5个人中任选2人排在甲、乙之间的两个位置上，有种方法，第二步，把甲、乙及中间2人看作一个元素与剩下的3个人作全排列，有种方法，第三步，对甲、乙进行全排列，故共有

种不同站法。

（4）方法一：男生站在前4个位置上有种站法，女生站在后三个位置上有种站法，男女生站成一排是分两步完成的，因此这种站法共有种，而女生站在前三个位置上，男生站在后四个位置上也有种站法，这两种站法都符合要求，所以四名男生站在一起，三名女生也站在一起的站法共有

种。

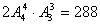
方法二：把站在一起的四名男生看作一个整体，站在一起的女生也看成一个整体，这样解决这个问题可分为三个步骤：选排男生、女生这两个整体，有种排法，然后排四名男生，有种排法，最后排三名女生，有种排法，根据分步计数原理，将四名男生站在一起，三名女生站在一起的站法有

种。

（5）不妨先排男生，有种排法，在四名男生间的三个间隔共有三个位置安排三名女生，有种，因此共有种排法符合要求，故四名男生三名女生相间排列的排法共有

种。

（6）在7个位置上任意排列7名学生，有排法种，由于女生的顺序一定，而在中每一种情况均以计算，故三名女生顺序一定的排法有

种。

例10、某班开设的课程有语文、数学、英语、政治、物理、化学、生物、体育共8门。若星期一上午排4节不同的课，并且规定体育课不能排在第一节及第四节，那么星期一上午该班的课程表有多少种不同的排法？

解：若不排体育课，则有

种方法；若排体育课，则有

种方法。

故共有

种不同的排法。

,