中考几何代数综合题（中考热点顺藤摸瓜）

多年来中考试题中，数与代数综合问题经久不衰，它常常涉及数与式、方程与不等式、函数与图像、应用与探索等多方面的内容。大家普遍认为它具有综合性强、区分度高、难度大等特点。往往所涉及的知识点多、技巧性强、覆盖面大。

解答这类问题的关键是正确理解题目中的已知与未知之间的关系。运用不等式的性质、方程的解法或根的判别式与根与系数关系、函数图像位置特性以及增减性等进行综合分析，其间往往一般还需要进行分类讨论才可完满求解问题。

类型1 数与式难题，灵活巧解源于代数式的融会贯通

例1．（南通中考题）已知x＝2m n 2和x＝m 2n时，多项式x² 4x 6的值相等，且m﹣n 2≠0，则当x＝3（m n 1）时，多项式x² 4x 6的值等于______．

【思路1】把x＝2m n 2和x＝m 2n分别代入多项式x² 4x 6中，由相等关系，(2m n 2)² 4(2m n 2) 6=(m 2n)² 4(m 2n) 6,化简得（m-n 2）(3m 3m 6)=0, 因m﹣n 2≠0，所以3m 3m 6=0，x=-3, 代入多项式x² 4x 6可求得值为3.

【思路2】取m=0, 则x＝n 2和x＝2n，别代入多项式x² 4x 6中，由相等关系，可得n=-2,再把m=0, n=-2,代入x＝3（m n 1）=-3，代入所求式同样求出结果。

【思路3】先将x＝2m n 2和x＝m 2n时，多项式x² 4x 6的值相等理解为x＝2m n 2和x＝m 2n时，二次函数y＝x² 4x 6的值相等，

∴3m 3n 2＝﹣4，m n＝﹣2，

∴当x＝3（m n 1）＝3（﹣2 1）＝﹣3时，

x² 4x 6＝（﹣3）2 4×（﹣3） 6＝3．

故答案为：3．

类型2 方程型难题，依据已知条件，顺藤摸瓜，灵活转化条件是这类问题常用策略

例2. （荆州中考题）已知关于x的一元二次方程x² （k﹣5）x 1﹣k＝0，其中k为常数．

（1）求证：无论k为何值，方程总有两个不相等实数根；

（2）已知函数y＝x² （k﹣5）x 1﹣k的图象不经过第三象限，求k的取值范围；

（3）若原方程的一个根大于3，另一个根小于3，求k的最大整数值．

【分析】（1）求出方程的判别式△的值，利用配方法得出△＞0，根据判别式的意义即可证明；

（2）由于已知二次函数图像不经过第三象限，又△＝（k﹣5）²﹣4（1﹣k）＝（k﹣3）² 12＞0，所以抛物线的顶点在x轴的下方经过一、二、四象限，根据二次项系数知道抛物线开口向上，由此可以得出关于k的不等式组，解不等式组即可求解；

（3）设方程的两个根分别是x1，x2，根据题意得（x1﹣3）（x2﹣3）＜0，根据一元二次方程根与系数的关系求得k的取值范围，再进一步求出k的最大整数值．

【解答】（1）证明：∵△＝（k﹣5）²﹣4（1﹣k）＝k²﹣6k 21＝（k﹣3）² 12＞0，∴无论k为何值，方程总有两个不相等实数根；

（2）解：∵二次函数y＝x² （k﹣5）x 1﹣k的图象不经过第三象限，二次项系数a＝1，∴抛物线开口方向向上，

∵△＝（k﹣3）² 12＞0，∴抛物线与x轴有两个交点，

设抛物线与x轴的交点的横坐标分别为x1，x2，

∴x1 x2＝5﹣k＞0，x1•x2＝1﹣k≥0，解得k≤1，

即k的取值范围是k≤1；

（3）解：设方程的两个根分别是x1，x2，

根据题意，得（x1﹣3）（x2﹣3）＜0，即x1•x2﹣3（x1 x2） 9＜0，

又x1 x2＝5﹣k，x1•x2＝1﹣k，

代入得，1﹣k﹣3（5﹣k） 9＜0，解得k＜5/2．

则k的最大整数值为2．

【点评】本题考查了抛物线与x轴的交点，二次函数的图象和性质，二次函数与一元二次方程的关系，根的判别式，根与系数的关系，综合性较强，难度适中．

例3.（乐山中考题）已知关于x的一元二次方程mx² （1﹣5m）x﹣5＝0（m≠0）．

（1）求证：无论m为任何非零实数，此方程总有两个实数根；

（2）若抛物线y＝mx² （1﹣5m）x﹣5与x轴交于A（x1，0）、B（x2，0）两点，且|x1﹣x2|＝6，求m的值；

（3）若m＞0，点P（a，b）与Q（a n，b）在（2）中的抛物线上（点P、Q不重合），求代数式4a²﹣n² 8n的值．

【分析】（1）直接利用△＝b²﹣4ac，进而利用偶次方的性质得出答案；

（2）首先解方程，进而由|x1﹣x2|＝6，求出答案；

（3）利用（2）中所求得出m的值，进而利用二次函数对称轴得出答案．

【解答】（1）证明：由题意可得：

△＝（1﹣5m）²﹣4m×（﹣5）

＝1 25m²﹣10m 20m＝25m² 10m 1＝（5m 1）²≥0，

故无论m为任何非零实数，此方程总有两个实数根；

（2）解：mx² （1﹣5m）x﹣5＝0，

（x﹣5）（mx 1）＝0，解得：x1＝﹣1/m，x2＝5，

由|x1﹣x2|＝6，得|﹣1/m﹣5|＝6，

解得：m＝1或m＝﹣1/11；

（3）解：由（2）得，当m＞0时，m＝1，

此时抛物线为y＝x²﹣4x﹣5，其对称轴为：x＝2，

由题已知，P，Q关于x＝2对称，

∴(a a 2)/2＝2，即2a＝4﹣n，

∴4a²﹣n² 8n＝（4﹣n）²﹣n² 8n＝16．

类型3 函数难题，通过关键点坐标纽带特性，融会贯通方程、不等式与函数知识三者之间联系，是解决函数必要条件及常用策略。

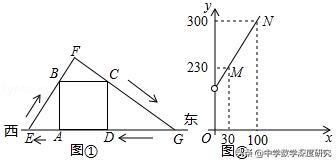
例4．（苏州中考题）如图①，直线l表示一条东西走向的笔直公路，四边形ABCD是一块边长为100米的正方形草地，点A，D在直线l上，小明从点A出发，沿公路l向西走了若干米后到达点E处，然后转身沿射线EB方向走到点F处，接着又改变方向沿射线FC方向走到公路l上的点G处，最后沿公路l回到点A处．设AE＝x米（其中x＞0），GA＝y米，已知y与x之间的函数关系如图②所示，

（1）求图②中线段MN所在直线的函数表达式；

（2）试问小明从起点A出发直至最后回到点A处，所走过的路径（即△EFG）是否可以是一个等腰三角形？如果可以，求出相应x的值；如果不可以，说明理由．

【分析】（1）根据点M、N的坐标，利用待定系数法即可求出图②中线段MN所在直线的函数表达式；

（2）分FE＝FG、FG＝EG及EF＝EG三种情况考虑：①考虑FE＝FG是否成立，连接EC，通过计算可得出ED＝GD，结合CD⊥EG，可得出CE＝CG，根据等腰三角形的性质可得出∠CGE＝∠CEG、∠FEG＞∠CGE，进而可得出FE≠FG；②考虑FG＝EG是否成立，由正方形的性质可得出BC∥EG，进而可得出△FBC∽△FEG，根据相似三角形的性质可得出若FG＝EG则FC＝BC，进而可得出CG、DG的长度，在Rt△CDG中，利用勾股定理即可求出x的值；③考虑EF＝EG是否成立，同理可得出若EF＝EG则FB＝BC，进而可得出BE的长度，在Rt△ABE中，利用勾股定理即可求出x的值．综上即可得出结论．

【解答】（1）设线段MN所在直线的函数表达式为y＝kx b，

将M（30，230）、N（100，300）代入y＝kx b，

30k b=230,100k b=300，解得：k=1, b=200，

∴线段MN所在直线的函数表达式为y＝x 200．

（2）分三种情况考虑：

①考虑FE＝FG是否成立，连接EC，如图所示．

∵AE＝x，AD＝100，GA＝x 200，∴ED＝GD＝x 100．

又∵CD⊥EG，∴CE＝CG，∴∠CGE＝∠CEG，

∴∠FEG＞∠CGE，∴FE≠FG；

②考虑FG＝EG是否成立．

∵四边形ABCD是正方形，∴BC∥EG，∴△FBC∽△FEG．

假设FG＝EG成立，则FC＝BC成立，∴FC＝BC＝100．

∵AE＝x，GA＝x 200，∴FG＝EG＝AE GA＝2x 200，

∴CG＝FG﹣FC＝2x 200﹣100＝2x 100．

在Rt△CDG中，CD＝100，GD＝x 100，CG＝2x 100，

∴100² （x 100）²＝（2x 100）²，

解得：x1＝﹣100（不合题意，舍去），x2＝100/3；

③考虑EF＝EG是否成立．

同理，假设EF＝EG成立，则FB＝BC成立，

∴BE＝EF﹣FB＝2x 200﹣100＝2x 100．

在Rt△ABE中，AE＝x，AB＝100，BE＝2x 100，

∴100² x²＝（2x 100）²，

解得：x1＝0（不合题意，舍去），x2＝﹣400/3（不合题意，舍去）．

综上所述：当x＝100/3时，△EFG是一个等腰三角形．

【点评】本题考查了待定系数法求一次函数解析式、等腰三角形的判定与性质、相似三角形的判定与性质、正方形的性质以及勾股定理，解题的关键是：（1）根据点的坐标，利用待定系数法求出一次函数关系式；（2）分FE＝FG、FG＝EG及EF＝EG三种情况求出x的值．

例5（资阳中考题）如图，已知直线l分别与x轴、y轴交于A，B两点，与双曲线y＝a/x（a≠0，x＞0）分别交于D、E两点．

（1）若点D的坐标为（4，1），点E的坐标为（1，4）：

①分别求出直线l与双曲线的解析式；

②若将直线l向下平移m（m＞0）个单位，当m为何值时，直线l与双曲线有且只有一个交点？

（2）假设点A的坐标为（a，0），点B的坐标为（0，b），点D为线段AB的n等分点，请直接写出b的值．

【解析】（1）①把D（4，1）代入y＝a/x得a＝1×4＝4，

所以反比例函数解析式为y＝4/x（x＞0）；

设直线l的解析式为y＝kx t，

化为关于x的方程得x² （m﹣5）x 4＝0，

△＝（m﹣5）2﹣4×4＝0，解得m1＝1，m2＝9，

而m＝9时，解得x＝﹣2，故舍去，

所以当m＝1时，直线l与双曲线有且只有一个交点；

（2）作DF⊥x轴，如图，

∵点D为线段AB的n等分点，∴DA：AB＝1：n，

∵DF∥OB，∴△ADF∽△ABO，

∴AF/AO=DF/BO=AD/AB，即AF/a=DF/b=1/n，

∴AF＝a/n，DF＝b/n，∴OF＝a﹣ a/n，∴D点坐标为（a﹣a/n ，b/n），

方法总结：从以上5个例题我们不难体会到这类问题求解策略，"顺藤摸瓜"，通俗地讲就是在阅读题干的时候，每出现一个条件，就必须大胆联想有这个条件能推导出什么结论，得出的结论对解题所求结果有什么帮助，还可继续拓展得到什么，想办法沟通靠拢。

,