如何证明存在唯一极值点（同时不满足极值三个充分条件的点）

如果函数在一个点上，同时不能满足极值的三个充分条件，那么这个点还有可能是极值点吗？换句话说，函数是否存在同时不满足极值三个充分条件的极值点。看完下面这道关于分段函数的极值问题，您就会明确这个问题了。

设{当x不等于0时，f(x)=x^4sin^2(1/x)；当x=0时，f(x)=0}.

(1)证明x=0是函数f的极小值点;

(2)说明在f的极小值点x=0处是否满足极值的第一充分条件或第二充分条件.

分析：(1)这个分段函数在x=0连续，但却不可导，即x=0是函数的不可导点。如果您要用极值的第一充分条件来判定它是不是极值点的话，那是行不通的。不信您可以自己动手试一试。这时候我们可以用极值的定义来判断。即在x=0的某邻域上，所有的函数值都不小于f(0)，就称x=0是函数的极小值点，反之则是极大值点。事实上，这道题所取的这个邻域甚至可以是全域R。

(2)之所以(1)中不能运用极值的第一充分条件来判定x=0是否函数的极值点，就是因为函数在这个点上，并不满足第一充分条件。想要证明这一点，仍需对函数求导。然后证明函数在x=0的所有单侧(左侧或右侧，未必要左侧和右侧同时满足)邻域内，导函数值总是存在变号的情况，就可以了。即在任一左侧邻域内，或任一右侧邻域内，肯定同时存在负导数和正导数。

证：(1)∵对任意x≠0，有f(x)=x^4sin^2(1/x)≥0，∴x=0是f的极小值点.

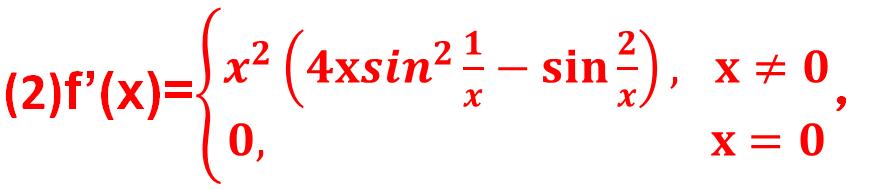
(2){当x不等于0时，f'(x)=x^2(4xsin^2(1/x)-sin(2/x))；当x=0时，f'(0)}；

【导函数仍是一个分段函数。这个导函数也是连续但在x=0不可导的，下面补充x不等于0时的求导过程：f'(x)=4x^3sin^2(1/x)-2x^4cos(1/x)sin(1/x)/x^2

=4x^3sin^2(1/x)-x^2sin(2/x)=x^2(4xsin^2(1/x)-sin(2/x)】

令xn=(2nπ π/4)^(-1), yn=(2nπ π/2)^(-1), (n=1,2,…)，【高等数学利用三角函数的周期性，取无穷大或无穷小量，以达到证明极小区间上的条件，是非常常见的方法】

则xn, yn>0且lim(x->无穷大)xn=lim(x->无穷大)yn=0，【说明xn, yn做自变量时，都是x=0任意右邻域内可以取得的点】

又f’(xn)=(2nπ π/4)^(-2)·[2(2nπ π/4)^(-1)-1]<0，

f’(yn)=(2nπ π/2)^(-2)·[4(2nπ π/2)^(-1)-0]=4(2nπ π/2)^(-3)>0，

即f’在任一U ⁰(0,δ)内变号，∴f在x=0处不满足第一充分条件.

又f”(0)=0，∴f在x=0处不满足第二充分条件.

甚至f^(n)(0)=0，∴f在x=0处不满足第三充分条件.

因此，可以发现，就算是一个点同时不能满足极值的三个充分条件，它也有可能是极值点。所以极值三个充分条件的逻辑或，并不是极值的必要条件.