八下人教版数学知识点（8下数学期末复习精准透视）

对于初中学生，数学复习至关重要，会不会复习，直接影响期末考试的成绩。有家长说，我们讨厌应试，讨厌在考试前才努力。但我想说：考试前的复习本身就是一种能力的培养，快速学习也是一种能力的体现，这种学习能力与生活中的很多事情密不可分，不要因为社会的负面声音而误导了孩子。

数学期末复习的基本任务是抓住双基串成线，沟通联系连成片，温故知新补缺漏，融会贯通更熟练。复习的特点之一是理，对所学的知识要进行系统整理，；特点之二是通，融会贯通，理清知识的来龙去脉、前因后果。由于期末复习是对本学期所学过知识进行再学习的过程，复习面广量大，时间紧，内容多，为使复习更贴近实际，从而用较少时间达到较好的复习效果，为此鲜明提出复习常见考点难点易错点，通过典型问题深化对知识的理解。

一、二次根式

常见考点：

1.含二次根式的分式的有意义的条件

2.最简二次根式的及同类二次根式

3.二次根式的运算

易错题型：

1.化去分母中的根式（有理化因式）

2.二次根式比较大小

难点：化简求值

典型问题

【解析】本题考查的是二次根式的混合运算，掌握二次根式的性质、二次根式的混合运算法则是解题的关键． 选C．

二、一元二次方程

常见考点：

1.解一元二次方程

2.根的判别式与根的系数的简单应用

3.一元二次方程的应用【平均增长率，商品销售利润方案】

易错题型：

1.含参数的一元二次方程【检验根的判别式△以及二次项系数】

2.用配方法求最值。

难点：一元二次方程的综合应用

典型问题

＝1，而m﹣1≠0，∴m的值为3/2．

4．（2019•长沙）近日，长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意见》，鼓励教师参与志愿辅导，某区率先示范，推出名师公益大课堂，为学生提供线上线下免费辅导，据统计，第一批公益课受益学生2万人次，第三批公益课受益学生2.42万人次．

（1）如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率；

（2）按照这个增长率，预计第四批公益课受益学生将达到多少万人次？

5．（2019•秦淮区二模）某商店第一个月以每件100元的价格购进200件衬衫，以每件150元的价格售罄．由于市场火爆，该商店第二个月再次购进一批衬衫，与第一批衬衫相比，这批衬衫的进价和数量都有一定的提高，其数量的增长率是进价增长率的2.5倍，该批衬衫仍以每件150元销售．第二个月结束后，商店对剩余的50件衬衫以每件120元的价格一次性清仓销售，商店出售这两批衬衫共盈利17500元．设第二批衬衫进价的增长率为x．

（1）第二批衬衫进价为 元，购进的数量为 件．（都用含x的代数式表示，不需化简）

（2）求x的值．

【解析】（1）100（1 x），200（1 2.5x）；

（2）根据题意，得

200×（150﹣100） [150﹣100（1 x）][200（1 2.5x）﹣50] 50[120﹣100（1 x）]＝17500．

三、勾股定理

常见考点：

1. 勾股数：

2. 勾股定理运用【折叠】

3. 勾股定理逆定理的运用【判定直角求面积】

4. 等积法求高

典型问题

1.（2019•天津中考题）如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE、折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE＝5，则GE的长为 _____．

【解析】∵四边形ABCD为正方形，∴AB＝AD＝12，∠BAD＝∠D＝90°，

由折叠及轴对称的性质可知，△ABF≌△GBF，BF垂直平分AG，

∴BF⊥AE，AH＝GH，∴∠FAH ∠AFH＝90°，

又∵∠FAH ∠BAH＝90°，∴∠AFH＝∠BAH，

∴△ABF≌△DAE（AAS），∴AF＝DE＝5，

3．（2019•马鞍山二模）若正整数a，b，c（a＜b＜c）满足a2 b2＝c2，则称（a，b，c）为一组"勾股数"．

观察下列两类"勾股数"：

第一类（a是奇数）：（3，4，5）；（5，12，13）；（7，24，25）；…

第二类（a是偶数）：（6，8，10）；（8，15，17）；（10，24，26）；…

（1）请再写出两组勾股数，每类各写一组；

（2）分别就a为奇数、偶数两种情形，用a表示b和c，并选择其中一种情形证明（a，b，c）是"勾股数"．

【解析】（1）第一组（a是奇数）：9，40，41（答案不唯一）；

第二组（a是偶数）：12，35，37（答案不唯一）；

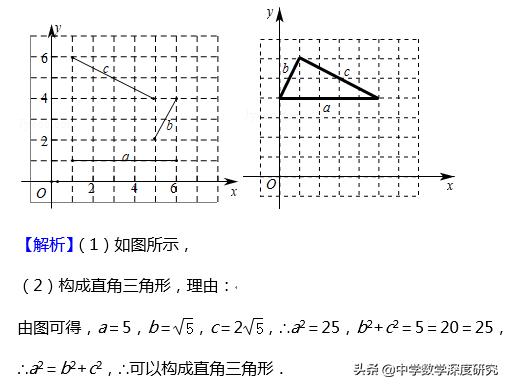
4．（2018秋•临安区期末）如图，平面直角坐标系中有三条线段a，b，c．

（1）请你平移其中两条线段，使得平移后的线段和第三条线段首位顺次相接，构成一个三角形（在网格内部完成构图）

（2）判断你构成的三角形的形状，并给出证明．

四、四边形

常见考点：

1.平行四边形、矩形、菱形、正方形的性质判定综合运用

2.中点四边形的运用

3.中位线的运用

4.斜边上的中线的运用

5.最值【由于菱形，矩形，正方形均为轴对称图形，所以大多最值问题是"将军饮马"】

6.辅助线的添加【倍增中线，补全图形，构造全等，截接，旋转等等】

典型问题

1．（2019•临沂中考题）如图，在平行四边形ABCD中，M、N是BD上两点，BM＝DN，连接AM、MC、CN、NA，添加一个条件，使四边形AMCN是矩形，这个条件是（ ）

A．OM＝1/2AC B．MB＝MO

C．BD⊥AC D．∠AMB＝∠CND

【解析】由平行四边形的性质可知：OA＝OC，OB＝OD，再证明OM＝ON即可证明四边形AMCN是平行四边形．故选：A．

2．（2019•本溪模拟）矩形ABCD中，AB＝8，AD＝6，P、Q是对角线BD上不重合的两点，点P关于直线AD，AB的对称点分别点E，F，点Q关于直线BC，CD的对称点分别是点G、H．若由点E，F，G，H构成的四边形恰好为菱形，则PQ的长为 ______．

【解析】根据轴对称求出AE＝AF＝AP，求出A、B、C、D都在菱形EFGH的边上，求出OA＝AP＝5，根据勾股定理求出ON，求出OP、OQ，即可得出答案为：5.6．

3．（2019•安徽中考题）如图，点E在▱ABCD内部，AF∥BE，DF∥CE．

（1）求证：△BCE≌△ADF；

（2）设▱ABCD的面积为S，四边形AEDF的面积为T，求S/T的值．

【解答】（1）∵四边形ABCD是平行四边形，

∴AD＝BC，AD∥BC，∴∠ABC ∠BAD＝180°，

∵AF∥BE，∴∠EAB ∠BAF＝180°，∴∠CBE＝∠DAF，

同理得∠BCE＝∠ADF，

在△BCE和△ADF中，∠CBE＝∠DAF，BC=AD,∠BCE＝∠ADF，

∴△BCE≌△ADF（ASA）；

（2）∵点E在▱ABCD内部，∴S△BEC S△AED＝1/2S▱ABCD，

由（1）知：△BCE≌△ADF，∴S△BCE＝S△ADF，

∴S四边形AEDF＝S△ADF S△AED＝S△BEC S△AED＝1/2S▱ABCD，

∵▱ABCD的面积为S，四边形AEDF的面积为T，∴S/T=S/(1/2S)＝2．

4．（2019•宁波中考题）如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．

（1）求证：BG＝DE；

（2）若E为AD中点，FH＝2，求菱形ABCD的周长．

【解答】（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，

∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，

∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，

∴△BGF≌△DEH（AAS），∴BG＝DE；

（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，

∵E为AD中点，∴AE＝ED，

∵BG＝DE，∴AE＝BG，AE∥BG，

∴四边形ABGE是平行四边形，∴AB＝EG，

∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．

难点破解策略总结

1. 几何证明是平面几何中的一个重要问题，它对培养学生逻辑思维能力有着很大作用。几何证明有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。

2. 掌握分析、证明几何问题的常用方法：

（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题的解决；

（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；

（3）综合分析法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。

3. 掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形，在构造基本图形时往往需要添加辅助线，以达到集中条件、转化问题的目的。

,