数学里的锯齿模型（特殊曲面在四维空间中仍保持不等价）

几十年来，数学家一直在寻找一对在四维空间中不能相互转换的特定曲面。现在他们找到了。

Seifert 曲面，就像这里显示的那样，是二维对象，其边界是数学（纽）结（knots）。

作者：Kevin Hartnett 2022-6-16

译者：zzllrr小乐 2022-6-16

在几何和密切相关的拓扑领域中，增加一个空间维度通常会产生奇妙的效果：以前不同的对象变得无法区分。但是一项新的证明发现，有些对象的差异是如此明显，以至于它们无法用更多的空间来消除（这些差异）。

该成果于 5 月底发布，解决了Charles Livingston在 1982 年提出的关于被称为 Seifert 曲面的二维对象的问题。Livingston知道，有许多成对的特定类型的 Seifert 曲面在位于三维空间的狭窄范围内时是不同的，但在有更多空间移动它们的四维空间中变得等价。

“拓扑学中很常见的事情是，当你有一些有趣的东西并添加额外的维度时，它可能不再有趣了，”斯坦福大学和克莱数学研究所的Maggie Miller说到。她与哥伦比亚大学的Kyle Hayden、首尔国立大学的Seungwon Kim 、韩国科学技术高等研究院的JungHwan Park和布林莫尔学院的Isaac Sundberg 一起是该新证明的合著者。

Livingston现在是印第安纳大学的名誉教授，他想知道移动到四维的一致化效果是否适用于所有这样的 Seifert 曲面对，或者是否有一些能够保持它们的独特性。

新工作确定了第一对 Seifert 曲面，它们在四维上与在三维上明显不同。它还更进一步，识别出在某些方面变得相似但在其他方面不相似的其他 Seifert 曲面对，从而阐明了四维空间的微妙复杂性。

要了解 Seifert 曲面，你首先需要了解纽结（knots），你可以将其视为绳子的闭合环。最简单的结只是一个圆圈。更复杂的结包括三叶形结和8字形结，其中绳子在与其末端连接在一起之前在其自身上下多次交叉。

结是一维对象，但它们构成了二维曲面的边界。再想想一个循环的绳子。该环形成了位于其内部的二维圆盘的边界。类似地，更复杂的结会成为更复杂的曲面的边界。Seifert 曲面就是边界为结的任何曲面。

此外，一个结可以是多个 Seifert 曲面的边界。一种查看方式是描绘曲面上的结的轨迹。它将曲面划分为两个互补的 Seifert 曲面。

一个两孔圆环一分为二。

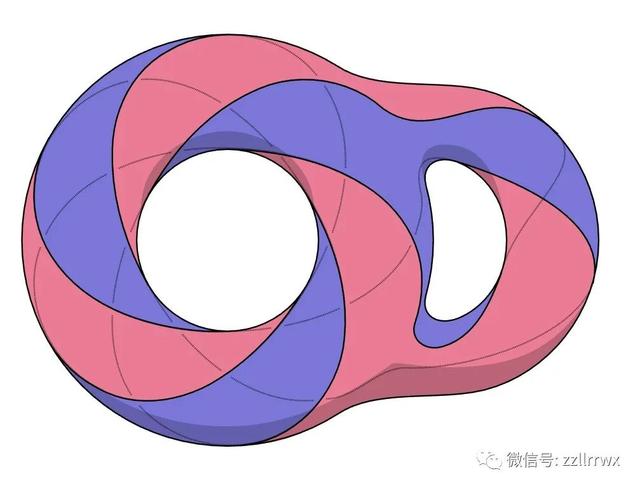
在双孔圆环曲面上描绘的结创建了两个互补的 Seifert 曲面，此处以粉红色和紫色显示。

Livingston 的问题是关于 Seifert 曲面之间的等价性。具体来说，他对可以逐渐变形以看起来彼此完全一样的曲面感兴趣，例如可以拉伸成椭圆形的圆盘。以这种方式可以使彼此完全相似的任何两个曲面称为同痕等价（isotopically equivalent）。

Livingston想知道是否存在任何来自同一个结（并且亏格相同——意味着它们具有相同数量的孔）的 Seifert 曲面对，它们在 3 维或 4 维空间中都不同痕。在随后的几十年里，数学家们找不到任何在传输到更高维度后幸存下来的三维差异。

“我提出了这个问题，长达40 年，”Livingston说。

Miller去年开始对这个问题感兴趣。今年四月，Miller、Hayden和Sundberg在罗德岛的普罗维登斯参加了一次会议，他们在一个深夜交谈。Miller提到了她、kim和Park为了证明Livingston猜想而想到的一对曲面。这些曲面于 1975 年首次被发现，虽然没有人证明它们在四维上是同痕的，但也没有人反驳它。这些曲面由一个有 19 个交叉点的纽结构成，看起来像彼此的偏移图像。

两个拜占庭 Seifert 曲面。

这些由同一个结形成的 Seifert 曲面不能在三维或四维上相互转换。

为了确定像一对曲面这样的拓扑对象是否等价，数学家使用了各种测试。这些称为不变量的测试有多种形式。有些运行起来更复杂，对对象的感知也更多；其他的更容易实现，但感知更少。

Hayden 和 Sundberg 最近使用称为 Khovanov 同调（Khovanov homology）的不变量进行了一些令人兴奋的工作，该不变量使用代数来提取有关对象如何组合在一起的信息。这些计算可能很难执行，而且对于非常复杂的对象——比如有数百个交叉点的结——它们非常困难。但是对于 Miller、Kim 和 Park 想到的结和相关的 Seifert 曲面，它们非常容易处理。然后，确定两个曲面是否等价就变成了比较计算每个曲面的 Khovanov 同调不变量时得到的数字的问题。

“如果你知道数字不同，你就知道曲面是不同的，”Khovanov 说，他在 1990 年代后期开发了他的同名技术。

Hayden 和 Sundberg 观察了 Miller 引起他们注意的这对 Seifert 曲面，并很快表明他们的 Khovanov 同调不变量不匹配，证明曲面是不同的。

“事实证明，这些例子确实隐藏了很长时间，”Hayden说。

在这一点上，数学家已经解决了Livingston的问题——确定了一对在三维空间中不同痕并且在四维空间中保持不变的Seifert曲面——但他们并没有就此止步。在Hayden和Sundberg的消息的鼓舞下，该小组决定看看他们是否可以使用更基本的不变量来证明相同的结果。他们做到了，使用了拓扑学中一种称为分支覆盖（branched covering）的基本技术。

普林斯顿大学的Patrick Naylor说：“他们用大约一页的数学来回答一个 40 年前的问题。” “这种情况并不经常发生。”

他们还继续确定了额外的 Seifert 曲面对，在四维空间中，它们在某种意义上不同痕（它们不是“光滑”同痕），但在另一种意义上是（它们是“拓扑”同痕）。这种拓扑等价和光滑等价之间的区别不适用于三维空间，并且是四维空间的深层奥秘之一——尽管现在对于 Seifert 曲面来说不那么重要了。

参考资料

论文

https://arxiv.org/abs/2205.15283

原文

https://www.quantamagazine.org/special-surfaces-remain-distinct-in-four-dimensions-20220616/