向量法求点面距离（向量法判断点与线段的关系）

如上图所示，有一点P和线段AB，已知点P的坐标和线段两个端点（A点和B点）的坐标。

通常会有以下几个问题：

1. 求线段AP在线段AB上的投影长度；
2. 求点P在线段AB上的投影点的坐标；
3. 判断点P的投影点是否在线段AB内；
4. 求∠PAB的角度值；
5. 判断∠PAB是锐角、直角，还是钝角。

对于上述问题，一种方法是通过几何 三角函数的方法来求解，相对繁琐复杂一些；而采用向量法，则相对简洁简单。

采用向量法，重点是需要理解向量点乘的数学定义和几何意义。

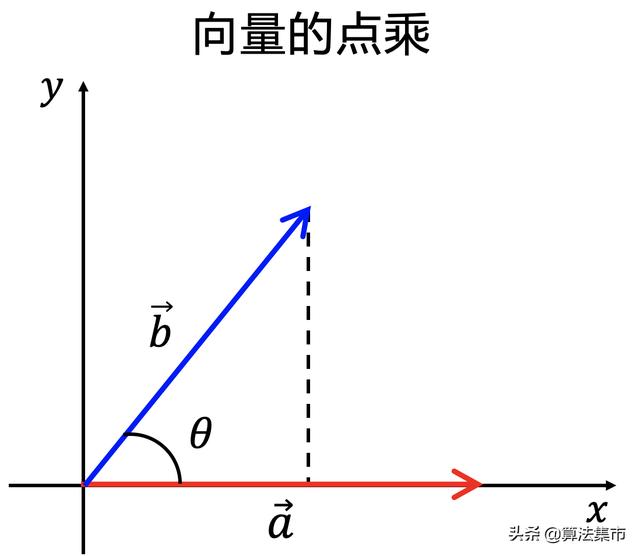
若把cos放到等式左侧，这个运算也可以理解为：在点乘运算中，b向量投影到a向量上（或a向量投影到b向量上，两者相同），然后通过除以它们的标量长度来“标准化”。这个值一定是小于等于1的，可以转化为一个角度值。

针对开始提到的五个问题，根据点P、点A、点B的坐标，转化为对应的向量，即可用向量点乘的几何意义来求解：

1、即为计算向量b在向量a方向上的投影长度（有正负之分）；

2、有了投影长度，除以向量a的标量长度，即得到点P的投影与线段AB的投影关系r；

• 若 r < 0：点P的投影点在点A方向上的延长线上；
• 若 r = 0：点P的投影点即为A点；
• 若 0 < r < 1：点P的投影点在线段AB内；
• 若 r = 1：点P的投影点即为B点；
• 若 r > 1： 点P的投影点在点B方向上的延长线上。

3、有了投影关系，再根据点A的坐标，即可求出点P投影点的坐标；

4、∠PAB即为两个向量之间的夹角；

5、判断∠PAB是锐角、直角，还是钝角，只需根据向量a和b的点乘结果来判断：

• 若 > 0：向量a和b的方向相同，∠PAB是锐角；
• 若 = 0：向量a和b正交，∠PAB是直角；
• 若 < 0：向量a和b的方向相反，∠PAB是钝角。

点P在不同的位置