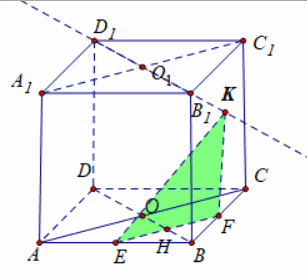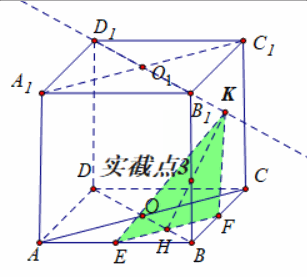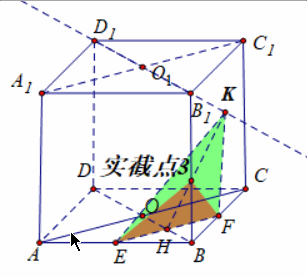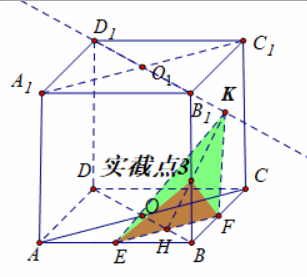
立体几何基本图（立体几何1.1:截面作图三步走）

1.1截面作图三

本文学习目标

1.掌握空间几何体截面作图方法

2.会判断空间几何体截面形状徐老师侃数学

作多面体截面方法

一、理论基础

1.定义及相关要素

用一个平面去截几何体，此平面与几何体的交集，叫做这个几何体的截面．此平面与几何体表面的交集(交线)叫做截线．此平面与几何体的棱（面）的交集(交点)叫做（实）截点.此平面与几何体的棱（面）的延长线的交点叫做虚截点．截面中能够确定的一部分平面叫做截小面.

2.作截面的宏观思路

找截点～～连截线～～围截面

3.作截面的一大思维误区

自我设限，忽略平面（直线）的无限延展性

4.作截面的理论依据

(1)确定平面的条件．

(2)如果两个不重合的平面有一个公共点，那么它们相交于过此点的一条直线．

(3)如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．

(4)如果一条直线平行于一个平面，经过这条直线的平面与这个平面相交，那么这条直线就和交线平行．

(5)如果两个平面平行，第三个平面和它们相交，那么两条交线平行．

5.作截面具体步骤

step.1找截点

方式1:延长截小面上一条直线，与几何体的棱、面（或其延长部分）相交，交点即截点

方式2:过一截点作另外两截点连线的平行线，交几何体棱于截点

注1：方式1中被延长的截小面上的直线，可以位于截小面外围（详见例1延长方式）；也可以位于截小面内部（详见例3延长方式）；具体选取哪条，取决于延长后，交点是否易于标识

注2:两种找截点方式的选择，取决于实际操作中哪种方式下的交点更易标识

step.2连截线

连接同一平面内的两个截点，成截线

step.3围截面

将各截线收尾相连，围截面

老师寄语：掌握思考问题的方式要比掌握一种解题方法重要

二、引例

1.如图，正方体中，、

、

分别在、

、

上，求作过、

、

三点的截面.

具体步骤：

step1.延长与交于虚截点1

step2.连接与虚截点1交于实截点1

说明：因为点及虚截点1都既在截面上又在多面体表面上，所以与虚截点1的连线即为截线，截线与侧棱的交点即为实截点1；

step3.延长与交于虚截点2

step4.连接与虚截点2交于实截点2

step5.顺次连接、实截点1、、

、

实截点2、围成截面.\

2.、

、

三点分别在直四棱柱的棱、

和上，试画出过、

、

三点的截面.

具体步骤：

step1.延长与交于虚截点1

step2.延长与交于虚截点2

step3.连接虚截点1与虚截点2交、

于实截点2、实截点1

step4.顺次连接Q、实截点2、、

围成截面.

3.试画出过正三棱柱的底边及两底中心连线中点的截面.

具体步骤：

step1.延长交实截点1

说明：此处延长，因为延长后的交点（截点）易于发现；反观延长，截点就不易于发现.

step2.过实截点1作平行线交棱、

于实截点2、实截点3；

说明：通过方式2找截点；原因：这道题通过方式2，交点（截点）更易标识

step3.顺次连接Q、实截点2、、

、

实截点3围成截面.

4.过正方体的中点、

作一个截面，使截面与底面所成的角为.则此截面的形状为（ ）

.三角形或五边形

.三角形或六边形

.六边形

.三角形或四边形

情况一：当截面前倾（如图4-1，点在之间）

具体步骤：

step1.过点作平行线交棱、

于实截点1、实截点2；（原因同例3.step2）

step2.延长与交于虚截点1

step3.连接实截点1与虚截点1交于实截点3

step4.延长与交于虚截点2

step5.连接实截点2与虚截点2交于实截点4

step6.顺次连接实截点1、实截点3、、、实截点4、实截点2、实截点1，围城截面六边形.

情况二：当截面后仰（如图4-2，点在正方体外部）

具体步骤：

step1.连接交棱于实截点1；（原因同例3.step1）

step2.顺次连接、实截点3、，围城截面三角形形.

综合情况一、情况二，截面的形状可能是六边形、三角形，故选.

关注微

,