几何法解圆锥曲线小题（圆锥曲线抛物线中阿基米德三角形学法指导）

高考数学压轴题压轴题系统讲解专栏第219课：高考数学圆锥曲线学法指导——抛物线的切线求法，线段长度比较大小问题。

本题考查的是直线与抛物线的位置关系，阿基米德三角形。

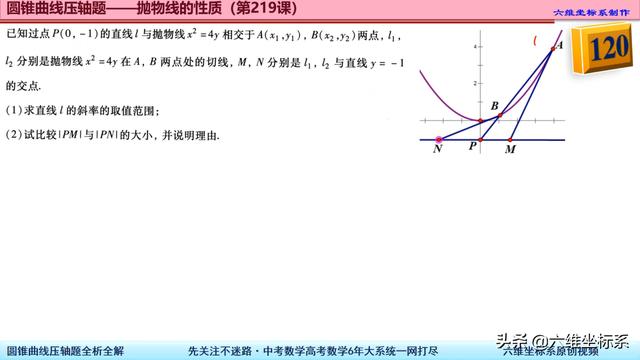
第一问，让我们求直线L的斜率的取值范围。我们就可以设点斜式，直线L与抛物线联立，由于有两个交点，所以判别式大于零，进而求出k的取值范围，相对来说比较简单。

第二问，让我们比较PM、PN的大小，那怎么办呢？我们可以求出M点和N点的坐标，M点的坐标就需要通过A点写出切线的方程。这个问题，我们在前面已经讲了很多，可以采用直接改写的方法，也可以借助导数去做，因为它是一个函数，所以说第一步。我们求导数，进而得到L1的斜率，然后借助点斜式，写出切线的方程，求出PM的距离。到这儿我们就要清楚了，如果求PN的话，用同样的方法。这两个长度求完以后，我们怎样处理呢？我们当然可以用作差法，也可以用作商法，本题采用作商法比较方便，为什么呢？大家思考一下。

然后借助非对称韦达定理的处理方法进行齐次化约分，大家做一下就会明白了。好，这个题目呢，我们就讲到这儿，下节课时间我们继续来研究阿基米德三角形的相关问题。系统学习请查看专栏：