小升初奥数浓度定义（海韵教育小升初）

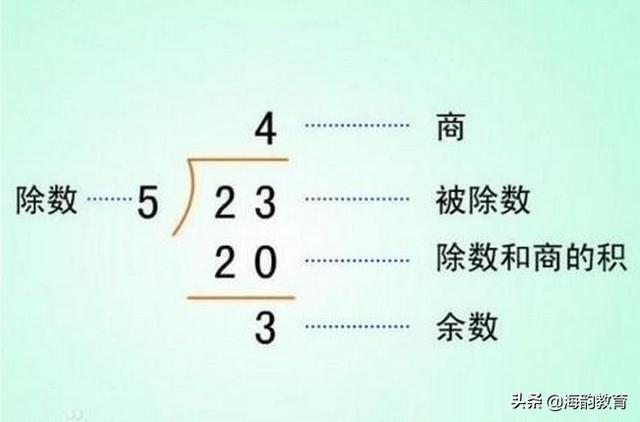
　　余数问题是小学奥数中的常见问题，今天我们来讨论一下余数的性质。同学们一定都知道，余数一定要比除数小，除此之外余数还有些什么样的性质呢？接下来我们边举例边总结。

　　例：

　　21÷5=4……1（21里面有4个5还多1）

　　33÷5=6……3（33里面有6个5还多1）

　　则有一：（21 33）÷5余（1 3）÷5

　　即当两个除法算式的除数相同都为A时，被除数之和除以A的余数，等于它们分别除以A时的余数之和除以A的余数。

　　则有二：（33-21）÷5余（3-1）÷5

　　即当两个除法算式的除数相同都为A时，被除数之差除以A的余数，等于它们分别除以A时的余数之差除以A的余数。

　　注意：当余数不够减时加上减数再减。

　　如：

　　24÷5余4

　　33÷5余3

　　则（33-24）÷5余（3 5-4 ）

　　则有三：（21×33）÷5余（1×3）÷5

　　即当两个除法算式的除数相同都为A时，被除数之积除以A的余数，等于它们分别除以A时的余数之积除以A的余数。

　　以上余数的三个性质需要同学们认真理解，明白原因才能熟练地运用。