阿基米德三角形在高考中的应用（抛物线中的阿基米德三角形应用篇）

以前跟一个排名挺不错的公立学校的数学聊过高三数学一轮复习时的进度，一轮复习事无巨细，无论题型难易程度如何，只要曾经在高考中考过就必须给学生讲到，因为谁也无法预料下一年高考中会不会出现，万一考到了而老师没讲到或者一带而过，那么误人子弟的罪名就算逃脱不了了，学生的角度和立场永远和老师是不同的，互相体谅一下吧。

其实高中数学中很多貌似超纲的内容都有学过，只是当时并不知道或者没有把与已知的内容产生关联性，老教材在必修二中学习直线与圆的时候会讲到圆的切点弦方程的求法，即便是新教材在选择性必修一直线与圆中依旧有这个内容，而过圆外一点P向圆作两条切线，切点设为A,B，求过A,B两点的直线方程高三的学生能不知道？在2020年全国1理科数学的第11题有一个这样的题目，如下：

题目用到了圆的切点弦方程，如果不知道该方程怎么写，那么本题大概率在规定时间内是解不出来的，如果将圆的切点弦扩展为椭圆，抛物线外一点作曲线的两条切线，求过两切点直线方程，这本质上和圆的切点弦方程的求法没有很大区别，将与此类似的内容整合起来这就是阿基米德三角形的应用了。

关于高中数学中抛物线与阿基米德三角形相关的内容最早在1998年就有期刊杂志提到了，由于电子版收录的原因，最早发布的会更早，如下图所示：

从1998年至今，高考中考查与此相关的内容不下十次，最近的一次在2021年全国乙卷理科数学，即便不知道阿基米德三角形这个概念，圆或抛物线的切线问题总归会是了解的，“筷子夹蛋”问题总会是了解的，二次曲线方程思想总会是了解的，圆锥曲线中与切线切点弦相关的题目肯定也遇到过做过的，所以别再说这是一个特定题型考过就不会再考的这种言论了。

上次内容中提到的与抛物线有关的阿基米德三角形的结论大多用在考试中的小题里面，由于其中涉及太多结论，在大题中并不能直接使用，但可辅助判定省略冗余过程，今天就以曾经考过的六道题目为例看看这个知识点的具体应用。

这是2018年新高考3卷的第16题，根据上期给出的性质可知点M在准线上，设出AB的中点N，则MN所在直线与y轴垂直，由于涉及中点和斜率，利用中点弦结论可轻易求出AB所在直线的斜率。

这是2014年的题目，根据结论可知AF和BF垂直，可直接求出BF所在直线的斜率。

本题考查上期中的第6个性质，|AF|·|BF|=|PF|²，点P所在直线已给出，只需求出点F到直线的距离即可，如不用结论，则需设出A,B两点坐标，用两纵坐标的和与积表示线段的长度，设出P点坐标，用P点坐标表示出AB所在直线方程，然后与抛物线联立，求出和与积，根据点P在已知直线上转化为一个变量求最值即可。

题目可以当成与线段长度有关的另一个结论，AB所在直线过焦点，则点P在准线上，P点的横坐标未知纵坐标已知，所求PF长度只与P点横坐标有关，而P点横坐标和AB中点的横坐标相同，即需根据AB长度求出AB中点的横坐标，利用AB的长度可求出AB中点的纵坐标，利用中点弦公式可确定出AB中点横纵坐标之间的关系，表示出AB中点横坐标后代入即可求出PF的长度。

第5题和第4题相似，用AB中点横坐标表示出AB的长度，用AB中点横坐标表示出PF的长度，最后用不等式即可求出所求式子的最值。

第6题是2021年全国乙卷理科数学，点P在确定的圆上，则P点横纵坐标的取值范围可知，设出点P的坐标，利用点P的坐标表示出AB所在直线的方程，然后按照的底乘高除二表示出三角形的面积，利用圆的方程将面积表示为一个变量的函数，求最值即可，过程如下：

但根据阿基米德三角形的相关结论，可用A,B两点坐标表示出P点的横纵坐标，再表示出AB所在直线的方程，用弦长公式求出AB的长度和点P到直线AB的距离，最后求出的三角形PAB的面积为A，B两点横坐标差的立方除以8p，在小题中可直接使用，过程如下：

在本题中x1,x2差的立方可直接转化为点P的横纵坐标，之后求函数最值即可，如下：

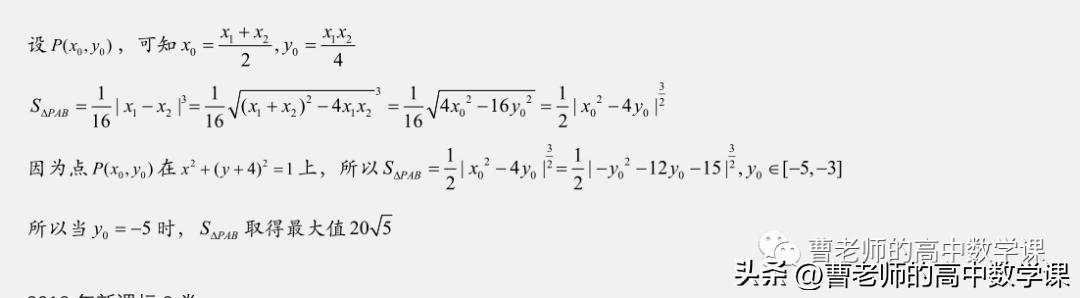
最后做一个总结，阿基米德三角形是以下几个知识的综合体，包括：

1. 圆的切点弦方程的求法
2. 思维训练37.抛物线中的切线问题
3. 【圆锥曲线专题】4.中点弦问题中两种求斜率的方法
4. 圆锥曲线中的双切线问题整理
5. 对二次曲线系方程用法的一点点补充
6. 圆锥曲线中与极点极线相关的基础知识