中考锐角三角函数应用讲解（河南中考锐角三角函数及其应用专项训练）

　锐角三角函数及其应用

类型一　仰角、俯角问题

1. (2015河南20题9分)如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°.若坡角∠FAE＝30°，求大树的高度．(结果保留整数．参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，根号3≈1.73)

【拓展猜押】如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120 m．求这栋高楼的高度. (结果用含非特殊角的三角函数及根式表示即可)

拓展猜押题图

2. (2014河南19题9分)在中俄“海上联合—2014”反潜演习中，我军舰A测得潜艇C的俯角为30°，位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度．(结果保留整数．参考数据：sin68°≈0.9，cos68°≈0.4，tan68°≈2.5，根号3≈1.7)

3. (2012河南20题9分)某宾馆为庆祝开业，在楼前悬挂了许多宣传条幅．如图所示，一条幅从楼顶A处放下，在楼前点C处拉直固定．小明为了测量此条幅的长度，他先在楼前D处测得楼顶A点的仰角为31°，再沿DB方向前进16米到达E处，测得点A的仰角为45°.已知点C到大厦的距离BC＝7米，∠ABD＝90°.请根据以上数据求条幅的长度(结果保留整数．参考数据：tan31°≈0.60，sin31°≈0.52，cos31°≈0.86)．

4. (2011河南19题9分)如图所示，中原福塔(河南广播电视塔)是世界第一高钢塔．小明所在的课外活动小组在距地面268 米高的室外观光层的点D处，测得地面上点B的俯角α为45°，点D到AO的距离DG为10 米；从地面上的点B沿BO方向走50 米到达点C处，测得塔尖A的仰角β为60°.请你根据以上数据计算塔高AO，并求出计算结果与实际塔高388 米之间的误差．(参考数据：根号3≈1.732，根号2≈1.414.结果精确到0.1 米)

类型二　坡度、坡角问题

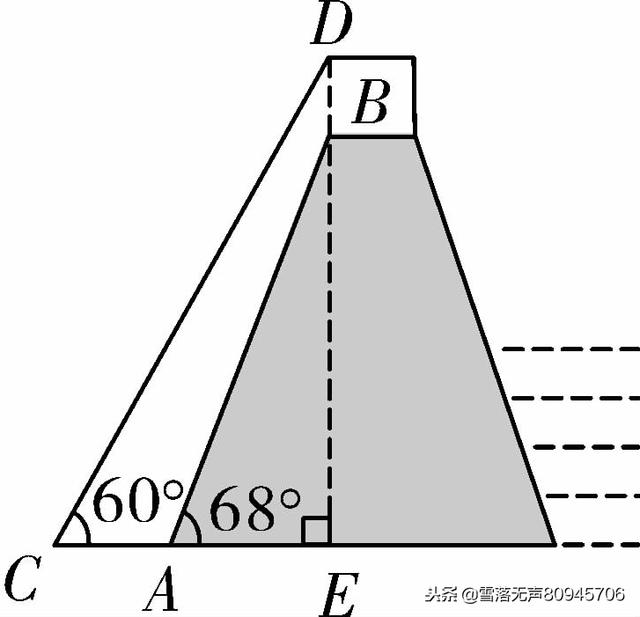
5. (2013河南19题9分)我国南水北调中线工程的起点是丹江口水库，按照工程计划，需对原水库大坝进行混凝土培厚加高，使坝高由原来的162米增加到

176.6米，以抬高蓄水位. 如图是某一段坝体加高工程的截面示意图，其中原坝体的高为BE，背水坡坡角∠BAE＝68°，新坝体的高为DE，背水坡坡角∠DCE＝60°. 求工程完工后背水坡底端水平方向增加的宽度AC(结果精确到0.1米．参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50，根号3≈1.73)

类型三　测量问题

6. (2009河南20题9分)如图所示，电工李师傅借助梯子安装天花板上距地面2.90 m的顶灯．已知梯子由两个相同的矩形面组成，每个矩形面的长都被六条踏板七等分，使用时梯脚

的固定跨度为1 m，矩形面与地面所成的角α为78°.李师傅的身高为1.78 m，当他攀升到头顶距天花板0.05～0.20 m时，安装起来比较方便．他现在竖直站立在梯子的第三级踏板上，请你通过计算判断他安装是否比较方便？(参考数据：sin78°≈0.98，cos78°≈0.21，tan78°≈4.70)

7. (2008河南20题9分)如图所示，A、B两地之间有条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达．现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC＝11 km，∠A＝45°，∠B＝37°，桥DC和AB平行，则现在从A地到B地可比原来少走多少路程？(结果精确到0.1km.参考数据：根号2≈1.41，sin37°≈0.60，cos37°≈0.80)

1. 有关锐角三角函数的实际应用的解题步骤：①审题：通读题干结合图形，在图中找出与题干相吻合的已知条件，弄明白哪些是已知量，哪些是未知量；

②构造直角三角形：将已知条件转化为示意图中的边角关系，再结合问题，把所求的量转化到与已知条件相结合的直角三角形中，若不能在图中体现，则需添加适当的辅助线将其结合；

③列关系式：在直角三角形中选择适当的锐角三角函数关系式进行求解；

④检验：解题完毕后，可能会存在一些较为特殊的数据，例如含有复杂的小数等.因此，要特别注意所求数据是否符合实际意义，同时还要注意结果有无要求保留的条件.

2. 在实际测量高度、宽度、距离等问题中，常结合视角知识构造“直角三角形”利用三角函数来解决问题，常见的构造的基本图形有如下几种：（1）构造一个直角三角形：

（2）构造两个直角三角形：

①不同地点测量：

②同一地点测量：