高数定积分计算公式（亲们交智商税了）

#创作挑战赛#

老黄之前其实已经推导过正割或余割的正整数幂的积分公式，就在《老黄学高数》系列学习视频的第268讲。利用的是高数教材《数学分析》中两者的递推公式。

不过老黄并非一个轻易满足的人，在《老黄学高数》第273讲，老黄证明了《数学分析》中要求证明的“正弦幂与余弦幂的积的不定积分的递推公式”。这个公式让老黄有了许多大胆的想法。第274讲，老黄利用它去推导了正弦或余弦的正整数幂的不定积分公式，这是老黄推导这组公式的第三种方法。下面老黄又想继续用它来推导正割或余割的正整数幂的积分公式。这是一个技术法。

老黄用图片的形式展示问题，这样看起来比较清晰：

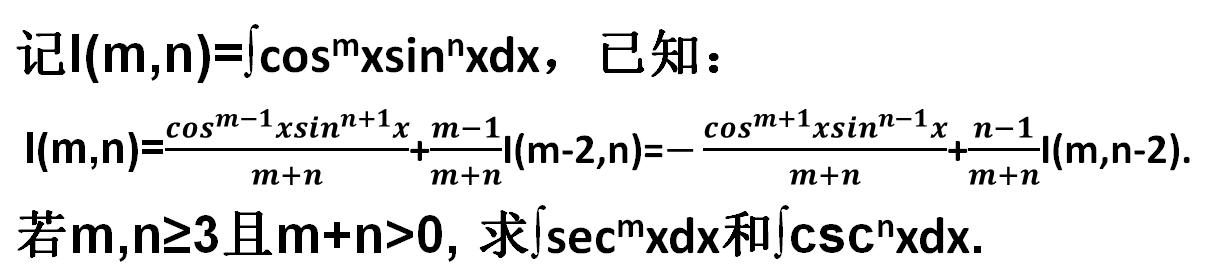
为了推导正割或余割的正整数幂，我们需要运用到正弦幂与余弦幂的积的不定积分的递推公式的负指数形式。因为正割和余割其实就是余弦和正弦的倒数，即负指数幂。并且需要将原公式反推一下。因为正整数幂的递推公式是使指数变小的，所以由I(m,n)推向I(m-2,n)或I(m,n-2). 而当指数为负时，我们就要反过来，往指数变大的方向递推，即从I(m-2,n)或I(m,n-2)推向I(m,n)，或者说，从I(m,n)推向I(m 2,n)或I(m,n 2). 这绝对是一个技术活哦。推导的过程以图片形式展示给大家如下：

因此老黄就从“正弦幂与余弦幂的积的不定积分的递减推导公式”得到了它的“递增推导形式”，重新组织问题如下：

注意，求∫(secx)^mdx，其实求的是I(-m,0)，而求∫(cscx)^ndx，则求的是I(0,-n). 都是直接运用上面的公式就可以搞定了。不过得到公式中的求和公式，特别是确定各项的系数，更加是一个技术活哦。

注意，由于当m=2时，(secx)^2的原函数是tanx C，所以第一个求和公式中只有k-1项。最后得到的公式组织成如下的形式：(为了保持与之前的形式可对照，这里暂时用n代替m)

与老黄之前推导的公式比较一下：

两者其实是可以互相转化的，一方面secxsinx=tanx; 另一方面只要将求和公式中的公因式提取出来，两组公式的形式就一模一样了。下面推导余割相关的公式，也是一个道理：

得到的公式，与之前得到的公式，形式上也是可以统一的：

其中cscxcosx=cotx，也可以把求和公式中的公因式提取出来，另外ln|cscx-cotx|=-ln|cscx cotx|.

最后是一道练习：求∫(secx)^2(cscx)^5dx.

解这道题需要三步：

1、先转化成I(-2,-5)的形式，运用指数递增的推导公式，化成I(0,-5)的表达式；

2、把I(0,-5)转化成∫(cscx)^5dx，然后运用余割的奇数次幂的不定积分公式；

3、把n=5, m=2代入公式，可展开，也可不展开。不过老黄还是展开了，目的是为了检验答案的正确性。

这个答案已经检验过了，检验这个答案同样也是一个技术活哦。我们甚至可以推导出正割的正整数幂乘余割的正整数幂的不定积分公式，那将是一个十分庞大的公式。喜欢看老黄高数作品的小伙伴，一定要相信自己，大胆地去尝试推导哦。就像老黄这么笨的人，都能做得到的，你没有理由做不到哦。