判断反比例函数和一次函数（一次函数与反比例函数的大致图像判断）

在北师大版的九年级数学课本上，有这么一道题：

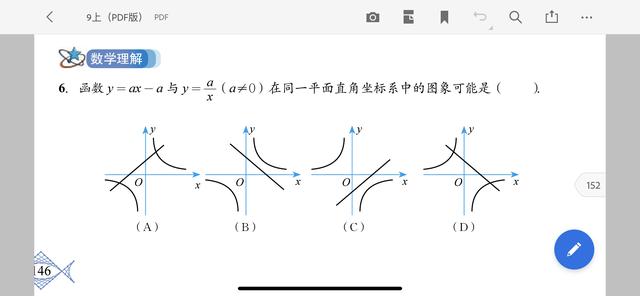
这种题型在考试中还是挺常见的，但是挺多学生会感觉无从下手。

今天我们就来说一说，这种题怎么解。

前置知识：函数的系数与图像之间的关系

这道题要我们判断可能的图象，条件是一个一次函数与一个反比例函数的表达式，而且这两个表达式中的系数大小不确定。

要想解决这道题，我们首先得知道，函数的系数与图象之间的关系。

一次函数的一般式是y=kx b（k≠0），其中k是一次项系数，b是常数项；它的图象是一条直线。

k的大小和这条直线的趋势有关。当k＞0，直线从左到右上升（y随x的增大而增大）；当k＜0，直线从左到右下降（y随x的增大而减小）。

b的大小和直线与y轴的交点有关。当b＞0，直线与y轴交点在原点的上方；当b＜0，直线与y轴的交点在原点的下方；当b＝0，图象经过原点。

反比例函数的一般式是y=k/x（k≠0），其中k是比例系数，它的图象是双曲线。

k的大小与双曲线的位置有关。当k＞0，双曲线分布在第一、三象限；当k＜0，双曲线分布在第二、四象限。

知识点搞定了，那这道题怎么解呢？和你分享两个思路。

思路1.画图象法：从系数出发，考虑可能的图象

既然系数不确定，那就对系数的大小进行分类讨论。

两个函数表达式的系数都跟a有关，而且a≠0，所以我们不妨分a＞0和a＜0两种情况来讨论。

如果a＞0，那么反比例函数的图象分布在第一、三象限；一次函数的图象从左到右向上，而且与y轴的交点在原点的下方。我画出来的草图是这样的：

对比四个选项，貌似没有匹配的。

那怎么办？试试另一种情况。

如果a＜0，那么反比例函数的图象分布在第二、四象限；一次函数的图象从左到右向下，而且与y轴的交点在原点的上方。我画出来的草图是这样的：

有没有发现，D选项跟草图很像？没错，答案就是D！

思路2.看图象法：从图象出发，考虑系数的范围

有的同学可能会说：“我不会画图象，怎么办？”

没关系，我们还有一个选择，就是看图象。通过观察四个选项，反过来推测系数的大小，然后排除存在矛盾的选项，剩下的就是正确答案。

对于上面这道题，我们可以用三个步骤进行处理：

第1步，标函数

拿红笔，在每个选项中的双曲线旁边标记反比例函数的表达式，在直线旁边标记一次函数的表达式。

第2步，写范围

回到A选项，双曲线分布在第一、三象限，说明y=a/x中的比例系数a＞0；直线从左到右向上，而且与y轴交点在原点上方，说明y=ax-a中的一次项系数a＞0，常数项-a＞0。

用同样的方法，把另外三个选项操作一遍，拿黑笔分别标上系数的范围，就可以进入下一步了。

第3步，找矛盾

再次回到选项A，我们在上一步写了三个范围：a＞0，a＞0和-a＞0，它们能不能同时成立呢？不能，因为把-a＞0两边同时除以-1，会变为a＜0，这跟前两个范围矛盾，所以选项A错误，排除。

同样的做法，我们可以发现，选项B和选项C都有矛盾，只有选项D没有矛盾，所以，正确答案是D。

两个思路相比，画图像法的要求高一些，看图像法对实力普通的同学或许更友好。

有的同学可能担心：“看图象法看起来挺简单，但是如果我用来解题，还是排除不了所有的错误选项，该怎么办？”

这时就需要从题目中，挖掘更多的线索。比如这一道题：

按照看图象法的三个步骤，标函数、写范围和找矛盾，我们会发现，选项C和选项D都有矛盾，但选项A和选项B都“没有”矛盾。

那怎么办？

进一步观察选项A和选项B，会发现，选项A的两个函数图象没有交点，而选项B的两个函数图象有交点。

那到底有没有交点呢？我们可以把这两个函数表达式联立起来，变成方程组，用代入法消元后，变成一元二次方程，再计算根判别式，就会发现，这个方程组没有实数解，说明两个函数的图象没有交点，于是正确答案就出来了，选A。

两个思路讲完了，你学会了吗？如果你有更好的办法，欢迎留言，期待你的分享！

,