宣布证明黎曼猜想的数学家（庞加莱猜想到微积分原理）

[遇见数学] 翻译制作小组将近期翻译和收集的视频制作了第 3 辑合集, 方便各位老师和朋友们观看收藏! 这里也附上前面两辑视频合集链接:

» 遇见数学翻译小组视频合集 第一辑

» 遇见数学翻译小组视频合集 第二辑

什么是黎曼猜想？

德国数学家波恩哈德·黎曼（Bernhard Riemann）于1859年在他的论文《论小于给定大数的素数个数》中提出了黎曼猜想。它是数学中一个重要而又著名的未解决的问题。多年来许多出色的数学家为之绞尽脑汁。2000年克雷数学研究所悬赏一百万美元奖金给予第一个得出正确证明的数学家。

黎曼猜想也是希尔伯特 23个 问题中唯一一个被收入克雷数学研究所的千禧年大奖难题，另一个难题P/NP问题的介绍，请点击这里链接。

黎曼猜想就是黎曼 ζ 函数：

非平凡零点（在此情况下是指s不为 -2、-4、-6‧‧‧等点的值）的实数部分是1/2. 更详细内容请见【遇见数学】翻译小组所译Numberphile的一段视频

观影链接>>>

什么是庞加莱猜想？

庞加莱猜想(Poincaré conjecture)最早是由法国数学家庞加莱于 1900 年提出的一个猜想：“任一单连通的、封闭的三维流形与三维球面同胚。” 也就是说，在三度空间里，任何一个封闭的，没有洞的形体，一定可以被捏成一个球。

这个猜想是克雷数学研究所悬赏的数学方面七大千禧年难题之一。

更多内容请见【遇见数学】翻译小组所译Numberphile一段视频中也有专门简短的介绍：

观影链接>>>

动画带你理解点积和叉积

点积 (dot product; scalar product, 也称为数量积). a.b = |a| |b| cos(θ)

点积其中一个非常实用之处可以判断两个向量的方向及角度.

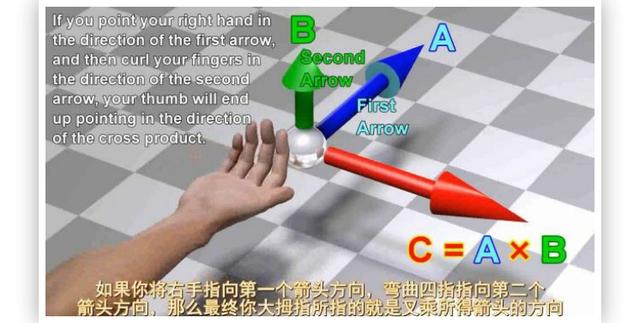
叉积的结果是一个新的向量, 这个新向量与前面两个向量垂直, 这在计算法线向量时非常有用. 另外新向量的长度是 |a×b|=|a| |b| sinθ , 在这里θ表示两向量之间的夹角, 0° ≤ θ ≤ 180° .

请看下面是 [遇见数学] 翻译小组带来的 4 分钟数学短片:

点积观影链接>>>

叉积观影链接>>>

微积分——现代科学的基础

17世纪下半叶牛顿与莱布尼兹两位伟大的数学家创立的微积分，开辟了新的数学领域。科学家以此工具解决了当时急待解决的天文学、航海学、力学、几何中众多问题。

微分和积分是互逆的两种运算，我们可以从汽车行驶速度、位移与时间关系出发，绘制出相应的图像，研究曲线的切线斜率和曲线下面积来分析出两个概念内在的相互联系。更多内容请看由 [遇见数学] 翻译小组译制的《微积分——现代科学的基础》视频：

观影链接>>>

复数及复变函数的动画解析

复数(Complex)作为实数的拓展历史悠久, 一度曾被叫做子虚乌有的数(imaginary), 直到十八世纪初经过棣莫弗及欧拉大力推动, 才被数学家们渐渐接受.

确实理解复数确实需要一点时间, 不过它并不复杂, 而且利用它还能画出非常美丽的变换和分形图形. 请看下面 [遇见数学] 翻译小组带来的《复数及复变函数动画解析》:

复数观影链接>>>

复变函数观影链接>>>

图论中的趣题：多少个警察才能抓到强盗？

在之前的视频《图论中警察抓强盗问题》里介绍了警察和强盗这个游戏, 并且说在图的某种结构下警察一定可以把强盗困在一个角落并且抓住它(cop-win), 又或者有时候强盗会永远逃避追捕(robber-win). 那么在这种情况下的平面图里, 增加最少多少个警察还是可以保证一定抓到强盗呢? 并且推广问题加上一点条件, 又会产生很多值得思考的新问题. 感兴趣的朋友可以查看下面链接以及后面 [遇见数学] 翻译小组制作的视频.

观影链接>>>

为什么 0的阶乘等于1 ?

一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。1808年，基斯顿·卡曼引进这个表示法。

也就是 n!=1×2×3×...×n。阶乘亦可以递归方式定义：0!=1，n!=(n-1)!×n。那么为什么 0!=1 呢? 请见【遇见数学】翻译小组带来 Numberphile的一段视频：

观影链接>>>

无限有多大?

无限！再也没有其他问题如此深刻地打动过人类的心灵。

——大卫·希尔伯特

如果你从无限中移走或添加一部分，剩下的还是无限。

——印度《夜柔吠陀》（公元前1200－900）

拉丁文中的无限是“infinitas”，意思是“没有边界”。那么它究竟有没有边界呢？这个问题不仅考问了 19 世纪末的数学界，还对许多现代数学的深层次研究产生着巨大的影响。下面 TED 这段关于"无限有多大?"的视频非常精彩，推荐观看：

观影链接>>>

数学创新高 Maths Raise Me Up | TEDx数学类演讲

数学的本质并非算数，而是寻找规律和研究关系的活动，也是提出和解决问题的艺术，更是思考的方式。资深国际讲师张宝幼以简单的10人分食7个蛋糕的问题考验在场观众的思考能力，举出唯有了解规律，才能打破规律，遵守原则却不被它所拘束。

观影链接>>>

感谢对[遇见数学]的关注和支持, 欢迎转发和留下精彩评论!

,