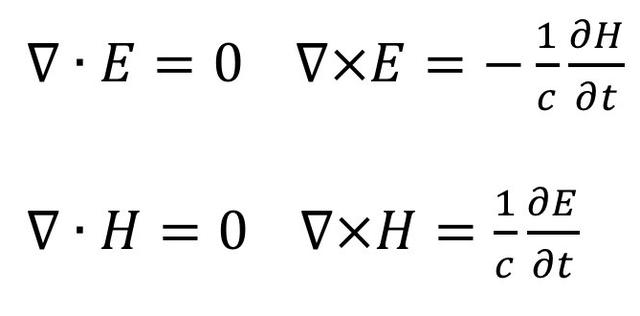人类最早发现的数学公式（这17个公式开启了人类文明的新阶段）

本文由公众号 “把科学带回家” 提供

给孩子最好的科学教育

作者 Ian Stewart等

编译 七君

知名数学科普作家、英国华威大学的荣誉数学教授伊安·斯图尔特（Ian Stewart）在《改变世界的17个方程》（17 Equations That Changed The World）中列举了人类科技史上17个最为重要的方程。可以说每一个方程都引领人类进入了科技和经济发展的新阶段。

从公元前530年到近代，这些方程叙述了人类理性从古至今的里程碑式进步。而一个人所受的科学教育越多，TA 往往会学习发明/发现时间离我们更近的方程。

那么，按照你对下面这些方程的了解程度，你的知识水平目前处于公元多少年呢？

勾股定理

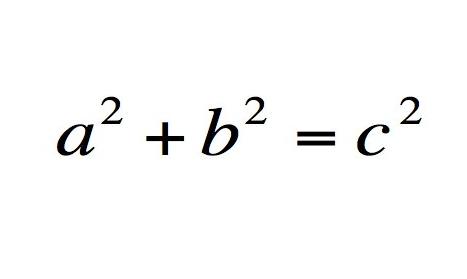
发明人/发现人：毕达哥拉斯/商高

发明/发现年代：公元前530年

勾股定理指的是，直角三角形的斜边的平方等于它的两条直角边的平方和。你会在初中接触到它。

勾股定理常被认为是毕达哥拉斯先发现的，但是现在关于谁是勾股定理的首个发现者还没有定论。也许古巴比伦人比毕达哥拉斯早1000年就领悟了勾股定理。

勾股定理是几何学的核心，它也是代数，还有三角学的基础。该公式对于测绘、制图、导航来说不可或缺。全球定位系统（GPS）就离不开勾股定理。

对数方程

约翰·纳皮尔（John Napier）

1610年

利用对数方程可以把乘法变为加法。你大概会在高一接触它。

对数方程最初是由苏格兰的一个地主约翰•纳皮尔（John Napier）在对大数进行乘法运算时发现的。纳皮尔你家是有多少地？

约翰•纳皮尔

对数是革命性的，它让繁琐的计算变得更方便快捷。在计算机出现前，工程师和天文学家靠这个方程让计算更快更准确。当然，计算机的出现让该对数方程逊色了不少，但是对于科学家来说对数方程仍然很重要。

对数方程还有相关的指数方程被用来进行数学建模，比如生物的生长，还有放射性衰变。

微积分

牛顿和莱布尼兹

1668年

微积分是计算瞬时变化量的数学工具。比如，物体运动的速度就可以用微积分来解决。你大概要在高中学习微积分的初级知识。

17世纪末，微积分由艾萨克•牛顿（Isaac Newton）和戈特弗里德•莱布尼茨（Gottfried Leibniz）在同一时期发现。至于谁先发现，谁又剽窃了谁，很长时间里两人争论不休，所以现在我们干脆说微积分是他俩发明的。

莱布尼茨（左）和牛顿（右）

斯图尔特认为，“微积分创造了现代世界”。微积分是测量线、面、体的关键。它也是许多自然法则的基础，也是微分方程的来源。

任何一个需要得出最优解的数学问题都涉及微积分。微积分是医学、经济学、物理学、工程学和计算机科学的必备知识。

万有引力定律

艾萨克·牛顿（Isaac Newton）

1687年

万有引力描述的是两个物体之间的引力和距离的关系。你大概要在高中学习这个知识。

艾萨克•牛顿利用翰尼斯•开普勒（Johannes Kepler）的天文学和数学研究得到了该定律。 但是，牛顿也有可能剽窃了同时代英国博物学家、发明家罗伯特•胡克（Robert Hooke）的研究。

在相对论出现之前，我们一直使用万有引力来描述世界是如何运行的。时至今日在卫星和探测器的轨道设计中我们依然需要应用万有引力。

在发射航天器时，我们用万有引力来寻找最佳的路径，节约航天器燃料。

波动方程

达朗贝尔(J- d’Almbert)

1746年

波动方程描述的是波的运动，比如小提琴琴弦的振动。你大概在大学学到（或者永远不会学到）。

波动方程可以解释声波的传播、地震的原理，以及海浪的行为。

石油公司在寻找油藏（石油勘探）时，常会引爆炸弹，然后利用波动方程来分析地质构造，从而锚定油藏所在地。

虚数

莱昂哈德·欧拉（Leonhard Euler）

1750年

虚数的平方为负1。你大概要在高中学习这个知识。

斯图尔特认为，“...如果没有虚数，很多现代科技，如电灯和数码相机都不可能发明。”虚数继续发展，就变成了数学的一支——复分析，工程师可以利用复分析来进行数据处理。

虚数广泛应用于电气工程学、信号处理和数学理论。

多面体欧拉定理

莱昂哈德·欧拉（Leonhard Euler）

1751年

多面体欧拉定理描述了一个多面体的顶点数V、棱数E及面数F间的关系。比如，一个立方体有8个顶点，12条棱，6个面，所以 8 6-12=2。你大概会在高中学到。

多面体欧拉定理是一个重要数学分支——拓扑学的基础。拓扑学研究的是平面连续形变后的几何性质。

在现代科学里，拓扑学可以用来研究 DNA 的功能，也可以用来研究社交媒体还有因特网。

正态分布

高斯(C. F. Gauss)

1810年

正态分布是一种钟形曲线，用来描述一个数值被观测到的概率。你大概在大学学到（或者永远不会学到）。

正态分布的钟形曲线

正态分布是现代统计学的基础，科学，尤其是医学、生物学和社会科学钟爱正态分布，也离不开正态分布。几乎对所有的科学实验数据的分析都离不开正态分布。

比如，利用正态分布可以确定在临床试验中，某个药物是否有效。

傅立叶变换

约瑟夫·傅里叶(J. Fourier)

1822年

傅立叶变换描述的是时间和频率的关系。你大概在大学学到（或者永远不会学到）。

傅立叶变换可以将成分复杂的波（比如歌曲、人的语言的声波）庖丁解牛，把它的成分一一分离出来。傅立叶变换对于信号分析来说至关重要。

傅立叶变换可以用来压缩文件。比如，一个音频文件可以被傅立叶变换分解成不同的声波，这样我们就可以去掉那些人类听不到的高音（高频波）和低音（低频波），从而精简文件。同理，可以利用傅立叶变换把图像压缩为 JPEG 格式。傅立叶变换也可以用来发现分子的结构。

纳维-斯托克斯方程

纳维和斯托克斯(C. Navier, G. Stokes)

1845年

纳维-斯托克斯方程是描述流体运动的基本方程。你大概在大学学到（或者永远不会学到）。

我们现在还不能完美地求解纳维-斯托克斯方程。谁能求解这个方程，就可以拿走著名的千禧年大奖，以及附带的一百万美金奖励。

好在现在的计算机的计算性能已经很强大，可以给出纳维-斯托克斯方程的近似解，所以物理学家和工程师才能研究复杂的流体问题，设计符合空气动力学的车辆和飞机。

麦克斯韦方程组

詹姆斯·麦克斯韦(J.C. Maxwell)

1865年

麦克斯韦方程组描述的是电场和磁场之间的关系。你大概在大学学到（或者永远不会学到）。

英国物理学家迈克尔•法拉第对电磁之间的关系做了开创性的研究，但由于数学不好，他并没有为这些现象做出数学上的解释。后来，詹姆斯•麦克斯韦把他的实验发现转化为方程，这就是麦克斯韦方程组的来源。

麦克斯韦方程组从根本上改变了物理学，它是电磁学的基础，现代电学和相关技术都依赖这个方程。有了它，才有雷达、电视和现代通信。

热力学第二定律

路德维希·玻尔兹曼(L. Boltzmann)

1874年

热力学第二定律描述的是，能量和热量随时间的推移而消散。热力学第二定律的基本概念你大概在初中会接触到，但是它的进阶知识你可能会在大学学习。

从左到右：墒增

热力学第二定律能解释能量和宇宙的变化。墒这个物理量也是基于热力学第二定律产生的。有了热力学第二定律，我们才能理解为什么热茶总是会变冷。

在设计引擎和发电厂的时候，必须要考虑热力学第二定律。在证明物质是由原子构成时，热力学第二定律也起到了一定的作用。

质能方程

阿尔伯特·爱因斯坦（Albert Einstein）

1905年

质能方程指的是，能量等于质量乘以光速的平方。你可能会在高中接触到它。

许多人都听说过质能方程，但是很少有人知道，在爱因斯坦之前，阿尔伯特·迈克耳孙（Albert Michelson）和爱德华·莫雷（Edward Morley）通过实验证明了光速守恒。而爱因斯坦则是在理论上解释了这个实验发现。

质能方程也许是历史上最著名的方程，它彻底改变了我们对宇宙和现实的看法。核武器的发明就依赖质能方程。

薛定谔方程

埃尔温·薛定谔(E. Schrodinger)

1927年

薛定谔方程是量子物理学的关键方程之一，它把物质描绘成了一种波。你大概在大学学到（或者永远不会学到）。

薛定谔

薛定谔方程彻底改变了我们对微观尺度的看法。薛定谔方程所描述的粒子以概率的方式出现，而且具有不确定性。薛定谔的观点是颠覆性的，而他的理论也成了量子力学的基础。

现在，核能、半导体、激光都和薛定谔方程有关。

信息论

克劳德·香农(C. Shannon)

1949年

克劳德·香农

信息论估计的是一段代码所包含的信息量。你大概在大学学到（或者永远不会学到）。

信息论可以用来估计任何内容（比如书和图片）的信息量。斯图尔特说，“这是信息时代的方程。”

利用信息论可以计算图片最多可以被无损压缩成多小。除了数据压缩以外，信息论也被广泛应用在密码学、数据传输等计算机科学中。

人口增长模型

罗伯特·梅（Robert May）

1975年

人口增长模型描述的是在资源有限的情况下，一群生物的数量增长模式。你大概在大学学到（或者永远不会学到）。

人口增长模型，横坐标为生长率，纵坐标为数量。在人口增长模型中，微小的初始条件变化，也会引发天差地别的后果。

人口增长模型和混沌理论有关，有助于解释自然现象。混沌理论中最广为人知的一个概念就是蝴蝶效应——微小的初始值变化会引起截然不同的后果，这就来自于人口增长模型。

现在，人口增长模型在地震预测和天气预报中都有应用。

布莱克-斯科尔斯方程

布莱克和斯科尔斯(F. Black, M. Scholes)

1990年

布莱克-斯科尔斯方程是为一类金融产品（如期货、期权）定价的数学模型。你大概在大学学到（或者永远不会学到）。

它的发明者——美国经济学家费希尔·布莱克（Fischer Black）和迈伦·舒尔兹（Myron Scholes）因为这个方程获得了1997年的诺贝尔经济学奖。

价值上万亿美金的金融产品都是布莱克-斯科尔斯方程的“衍生品”。许多人认为金融危机和布莱克-斯科尔斯方程脱不了干系，因为布莱克-斯科尔斯方程里包含的一些假设在现实生活中站不住脚。

在2008年的金融危机之后，实际上银行家们还在用布莱克-斯科尔斯方程对大多数金融衍生品进行定价。

你目前的数学水平晋级到了人类文明史的哪一关了呢，还是你已经通关了？

不过瘾，请戳

把科学带回家

ID：steamforkids

给孩子最好的科学教育

转载请联系 kids@huanqiukexue.com

长按二维码关注我们

图片非特别注明均来自网络。

为保护原创，参考资料储存于石墨：

https://shimo.im/docs/6DkPBgqk8NcHcOZy/

,