为什么同一液体不同高度压强不同？为什么液体在同一深度的各方向上的压强都相等

引言

初中物理课上，我们就知道：液体在同一深度的各方向上的压强都相等。

这个结论相当实用，可是我们还记得是怎么得到这个结论的呢？

不出意外，大部分同学都会说是通过实验得到的。

但是，大家不经常都说，在经典力学中，通过牛顿三大定律就可以推导出所有的力学结论吗？这里的液体压强属于流体静力学范畴，后者也属于经典力学，那么“在同一深度的各方向上的压强相等”这个结论是否可以推导出来呢？

流体的基本性质

气体和液体都是流体，流体有如下基本性质：

1. 流体是可压缩的。

初中我们就做过物理、化学实验，气体是可被压缩的，体积和压强满足相关规律。

液体特殊一点，压缩性比较小。

为简单起见，可以认为液体在压力情况下体积是没有变化的。

2. 流体是可任意分割的。分割的任意一块，都满足牛顿力学定律。

特别的：

如果是液体且处于平衡状态（如静止状态），那么分割的任意一块都与整体保持相同状态

证明

要证明各方向的压强相等，只需要按照下图证明Px=Py=Pz=Pn即可（其中Pn为指向任一方向的压强）即可。

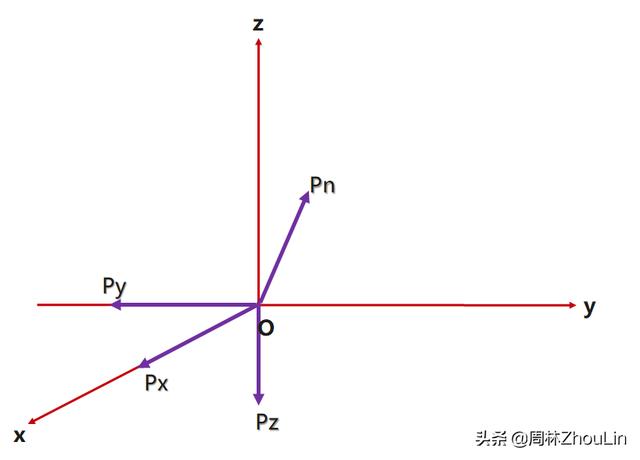
目前我们手里有的武器只有牛顿力学定律。所以我们需要利用受力分析来证明。

要证明压强的关系，又要利用受力分析，所以首先我们需要将压强转换成压力。

压力与压强的关系：

F=PS （式1）

F表示压力，P表示压强，S表示垂直于压强的受力面积。

把上面的受力面Sx、Sy、Sz和Sn拼接起来，就形成了一个封闭的四面体：

由上图所示：

Sx=S∆AOC Sy=S∆AOB Sz=S∆BOC Sn=S∆ABC （式2）

设ɑ是∆ABC与平面xOz的夹角，则∆AOB是∆ABC在平面xOz的投影，从而：

S∆AOB=S∆ABCcosɑ（式3）

这个四面体可以看做是整个流体的一部分。

显然，只有当这个四面体的体积足够小，是一个微元的时候，才能看做一个深度的质点，否则它本身有高度的话，那么就和题意要求的“某一深处”的条件矛盾了。

假设液体整体处于静止状态，那么这个四面体作为液体的一部分，根据上面的“流体基本性质2”可知，四面体也处于静止状态。

现在对该四面体进行受力分析：

除了它在四个面分别收到的压力之外，它还受到重力作用，其大小G=Mg

（其中M代表四面体的质量，g是重力加速度常量）

设液体的密度为ρ，则M=ρV，其中V是四面体体积。

V是受力面积与高的乘积，高与两个面的夹角相关，所以可以看出：

由于四面体是微元，所以受力面积趋向0、V是相对于受力面积的高阶无穷小。

从而可以推出：

推论1：G是相对于相对于Fz的高阶无穷小，忽略不计。

由上图：

在y轴方向上，合力应为0，所以：

Fy=Fncosɑ （式4）

将式1代入式4，得到：

PySy=PnSncosɑ （式5）

将式2代入式5，得到：

PyS∆AOB=PnS∆ABCcosɑ （式6）

将式3代入式6，得到：

Py=Pn

同理可证Px=Pn

结合推论1，也可证得Pz=Pn

从而有：Px=Py=Pz=Pn，命题得证。

总结

数学是一切自然科学的基础，大部分物理学结论其实都是根据思想实验 数学推导，得到大致方向性结论，然后再辅以实验进行验证。而并不是像很多人所想的那样——物理规律的发现完全来自没有方法与策略支撑的实验。

往期原创科普文章回顾：

《原创: 大神们是如何证明地球自转的》

《@李永乐老师：纠正一下“万有引力是如何被发现”的视频中的错误》

《原创: 抄起数学“瑞士军刀”——北大题也是小case》

别忘了点击文末广告，作为对作者原创的打赏和支持哦：），感谢！

,