高考数学理科椭圆题型（197:2013年广东卷理科数学抛物线切线）

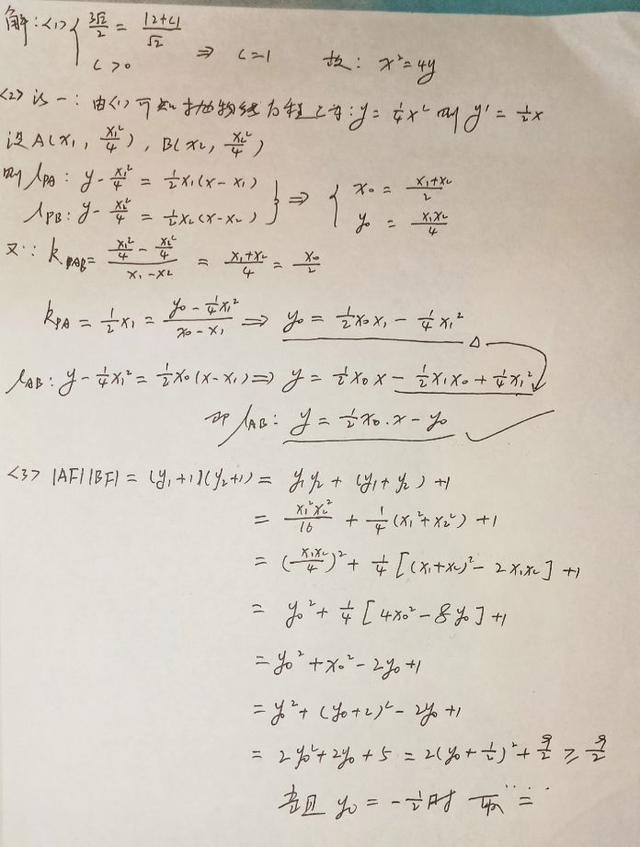
今天闲着没事写了写2013年广东卷的这个题，需要注意的是

第二问法二利用同构式，巧妙利用A在抛物线上把x1²转化为y1，然后利用P在直线上，同理可以得到关于B点的方程，又因为两点确定一条直线，A，B所在直线形式一致(同构式)。

第三问直线与抛物线联立看成关于x，y的方程，x0，y0当成常数利用韦达定理和抛物线定义即可。

最近几年貌似抛物线高考大题考察的不多，切线问题也考察不多，看到文章的学生不妨留意一下圆锥曲线中的双切线，(利用同构式，或者设点斜式，带入方程利用判别式＝0，得到关于斜率k的一元二次方程然后利用韦达定理等，)早些年地方卷高考考察过且间隔时间有点久，有兴趣的可以去搜搜早些年的真题，说不准今年就有可能出了呢，例如去年一卷的圆锥曲线题就是早些年江苏卷的题，(以上纯属个人瞎猜)[呲牙][呲牙][呲牙][呲牙][呲牙][呲牙]