异面直线所成的角的范围（直线与平面的夹角）

假设一条直线在一个平面上倾斜。平面的法线是从直线与平面接触的一点画出来的。这条法线和这条线成一个角。在解析几何中，直线与平面的夹角等于直线与法线夹角的补角。在本文中，我们将详细讨论这个概念。

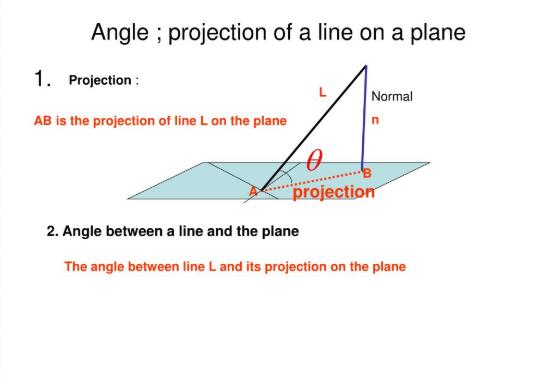
一条直线与平面成角Φ。 直线的向量方程可以表示成：

r = tb (r0是直线r上的一个点， b是直线r的平行向量，t是参数)

平面的矢量方程为：

r. n = 0 （n是平面的法向矢量，r是平面的上过法线交点的直线向量。）

设θ是直线与平面法线的夹角。其值利用两个向量的夹角公式，可由下式给出:

Φ是直线与平面的夹角，是90 - θ或θ的补角。我们知道cosθ= sin (90 - θ)所以Φ可以通过以下方式给出:

sinΦ=sin (90 – θ) = cos θ

举个例子更好理解这个问题：

空间的一条直线的方程是：

一个平面方程是：3x 4y – 12z = 7，求出它们的夹角。

解: 设θ是直线与平面法线的夹角。

因为直线过（0, -32, 2）这点， 而且其方向矢量为<6, 2, 3>

在矢量形式下，方程可以写成:

向量形式的平面方程可由:

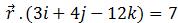
因此我们有直线的方向矢量b= 6i 2j 3k

和平面法向量 n= 3i 4j – 12k

带入向量夹角公式:

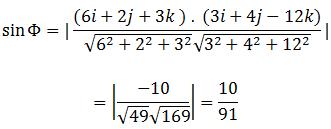
Φ 的值可有反函数求出：