python机器学习之决策树算法（Python实现机器学习算法）

朴素贝叶斯的一大特点就是特征的条件独立假设，但在现实情况下，条件独立这个假设通常过于严格，在实际中很难成立。

特征之间的相关性限制了朴素贝叶斯的性能，所以这里将继续介绍一种放宽了条件独立假设的贝叶斯算法——贝叶斯网络(Bayesian Network)。

贝叶斯网络的直观例子

先以一个例子进行引入。假设我们需要通过头像真实性、粉丝数量和动态更新频率来判断一个微博账号是否为真实账号。各特征属性之间的关系如下图所示：

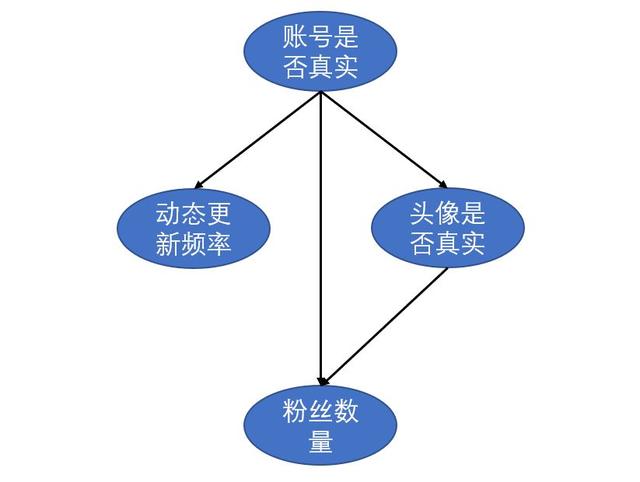
上图是一个有向无环图(DAG)，每个节点表示一个特征或者随机变量，特征之间的关系则是用箭头连线来表示，比如说动态的更新频率、粉丝数量和头像真实性都会对一个微博账号的真实性有影响，而头像真实性又对粉丝数量有一定影响。

但仅有各特征之间的关系还不足以进行贝叶斯分析。除此之外，贝叶斯网络中每个节点还有一个与之对应的概率表。

假设账号是否真实和头像是否真实有如下概率表：

第一张概率表表示的是账号是否真实，因为该节点没有父节点，可以直接用先验概率来表示，表示账号真实与否的概率。

第二张概率表表示的是账号真实性对于头像真实性的条件概率。比如说在头像为真实头像的条件下，账号为真的概率为0.88。

在有了DAG和概率表之后，我们便可以利用贝叶斯公式进行定量的因果关系推断。假设我们已知某微博账号使用了虚假头像，那么其账号为虚假账号的概率可以推断为：

利用贝叶斯公式，我们可知在虚假头像的情况下其账号为虚假账号的概率为0.345。

贝叶斯网络

上面的例子可以让大家直观地感受到贝叶斯网络的作用。一个贝叶斯网络通常由有向无环图(DAG)和节点对应的概率表组成。

其中DAG由节点(node)和有向边(edge)组成，节点表示特征属性或随机变量，有向边表示各变量之间的依赖关系。

贝叶斯网络的一个重要性质是：当一个节点的父节点概率分布确定之后，该节点条件独立于其所有的非直接父节点。这个性质方便于我们计算变量之间的联合概率分布。

一般来说，多变量非独立随机变量的联合概率分布计算公式如下：

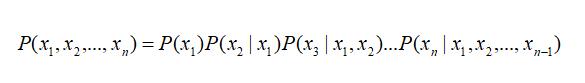
当有了上述性质之后，该式子就可以简化为：

基于先验概率、条件概率分布和贝叶斯公式，我们便可以基于贝叶斯网络进行概率推断。

基于pgmpy的贝叶斯网络实现

本节我们基于pgmpy来构造贝叶斯网络和进行建模训练。pgmpy是一款基于Python的概率图模型包，主要包括贝叶斯网络和马尔可夫蒙特卡洛等常见概率图模型的实现以及推断方法。本节使用pgmpy包来实现简单的贝叶斯网络。

我们以学生获得推荐信质量这样一个例子来进行贝叶斯网络的构造。具体走向图和概率表如下图所示：

考试难度、个人聪明与否都会影响到个人成绩，另外个人聪明与否也会影响到SAT分数，而个人成绩好坏会直接影响到推荐信的质量。下面我们直接采用pgmpy实现上述贝叶斯网络。

导入相关模块：

from pgmpy.factors.discrete import TabularCPD from pgmpy.models import BayesianModel

构建模型框架，指定各变量之间的依赖关系：

student_model = BayesianModel([('D', 'G'), ('I', 'G'), ('G', 'L'), ('I', 'S')])

构建各个节点和传入概率表并指定相关参数：

grade_cpd = TabularCPD( variable='G', # 节点名称 variable_card=3, # 节点取值个数 values=[[0.3, 0.05, 0.9, 0.5], # 该节点的概率表 [0.4, 0.25, 0.08, 0.3], [0.3, 0.7, 0.02, 0.2]], evidence=['I', 'D'], # 该节点的依赖节点 evidence_card=[2, 2] # 依赖节点的取值个数 ) difficulty_cpd = TabularCPD( variable='D', variable_card=2, values=[[0.6, 0.4]] ) intel_cpd = TabularCPD( variable='I', variable_card=2, values=[[0.7, 0.3]] ) letter_cpd = TabularCPD( variable='L', variable_card=2, values=[[0.1, 0.4, 0.99], [0.9, 0.6, 0.01]], evidence=['G'], evidence_card=[3] ) sat_cpd = TabularCPD( variable='S', variable_card=2, values=[[0.95, 0.2], [0.05, 0.8]], evidence=['I'], evidence_card=[2] )

将包含概率表的各节点添加到模型中：

student_model.add_cpds( grade_cpd, difficulty_cpd, intel_cpd, letter_cpd, sat_cpd )

获取模型的条件概率分布：

student_model.get_cpds()

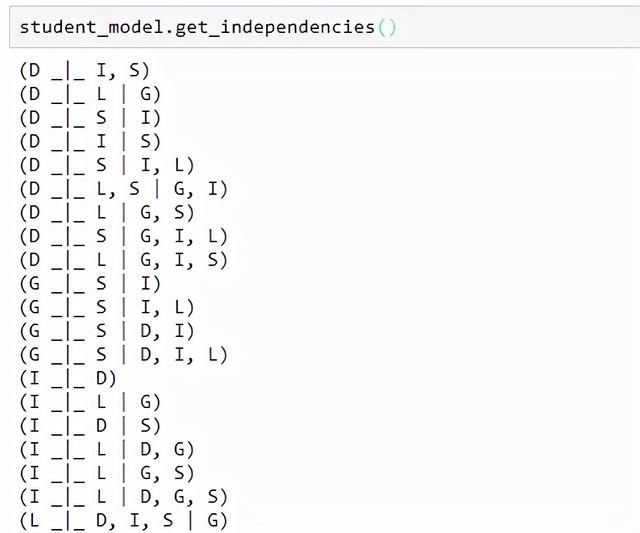
获取模型各节点之间的依赖关系：

student_model.get_independencies()

进行贝叶斯推断：

from pgmpy.inference import VariableElimination student_infer = VariableElimination(student_model) prob_G = student_infer.query( variables=['G'], evidence={'I': 1, 'D': 0}) print(prob_G)

可见当聪明的学生碰上较简单的考试时，获得第一等成绩的概率高达0.9。

除了以上构造贝叶斯网络的方法之外，我们还可以基于pgmpy进行数据训练。首先生成模拟数据并以上述的学生推荐信的模型变量进行命名：

# 生成数据 import numpy as np import pandas as pd raw_data = np.random.randint(low=0, high=2, size=(1000, 5)) data = pd.DataFrame(raw_data, columns=['D', 'I', 'G', 'L', 'S']) data.head()

然后基于数据进行模型训练：

# 定义模型 from pgmpy.models import BayesianModel from pgmpy.estimators import MaximumLikelihoodEstimator, BayesianEstimator model = BayesianModel([('D', 'G'), ('I', 'G'), ('I', 'S'), ('G', 'L')]) # 基于极大似然估计进行模型训练 model.fit(data, estimator=MaximumLikelihoodEstimator) for cpd in model.get_cpds(): # 打印条件概率分布 print("CPD of {variable}:".format(variable=cpd.variable)) print(cpd)

以上便是基于pgmpy的贝叶斯网络的简单实现。

原文参考资料：

pgmpy: Probabilistic Graphical Models using Python

数据挖掘导论

https://mp.weixin.qq.com/s/WtJ62UNyhIihpGsspDC7qQ

,