不小心把用户数据清除了怎么办?（卸下用户数据心防）

摘要： 区块链最核心的不可篡改和加密两项技术均来自于密码学的相关理论。 公钥密码技术和单向散列函数为比特币及其后区块链的发展奠定了条件。

— 密码学 公私钥 单向散列函数—

我们知道现在互联网除了信息的真实性之外，存在一个很大的问题就是用户产生增量数据的动力不足，上篇文章提到的留言板缺乏有效数据的情况就属于这种。

比如我们现在有很多网络借贷的平台，用户使用它们的服务时，在填写了必要的性别、年龄、收入等数据之外，如果平台还希望获得更多的辅助数据项进行信用评价，用户往往是不愿意提供的。

有的平台会采用奖券、返点等激励的方式驱动这些额外数据的收集（激励），或者进行非常翔实的解释工作（协调预期），但这样做并不十分有效——部分对隐私不敏感，或者价格优先型的客户除外。原因就在于没有可靠的加密技术的加持，用户并不能对平台完全信任，所以即使有了激励的承诺，出于安全的考虑，很多人也还是不愿意配合提供这些数据。

在与加密技术结合之后，激励与协调预期的方法才可以真正促进数据的生产和流动。由于数据权属不会受到平台方的威胁，而且产生的贡献可以追踪到个人，用户就可以更放心的通过提供数据来获得激励。设想在刚才网络借贷的场景，流程变更为产生的额外数据仅由用户单独保管，每一次用作借贷分析的需求都要用户提供特别的签名授权，而后再把数据使用产生的收益分成返还……

在这种情况下，数字世界的协作将更易达成。伴随个体加密技术的发展，将大大促进用户深度参与的热情，拓展我们现在社会的数据边界。而这种新型加密结构的搭建，也将帮助人类突破大数据、AI技术目前遇到的主要瓶颈，即多维度的真实可靠的数据源，成为其下一轮快速增长的必要条件。

不可篡改和加密技术的背后就是密码学，为了更清晰的说明这一点，让我们一起来了解一下这门学科。由于密码学的详细内容实在过于艰深复杂，涉及到大量的数学公式和逻辑推导，尤其是在与现代社会的计算机网络、量子等技术结合后，愈发变得庞杂而隐晦。因而在这里，我们只能稍稍讨论一些它的基本原理，并重点说明它和区块链之间的联系。

我们很多人都在有关战争的史料里见过一些涉及密码的情形。比如在古希腊城邦间的战役中两个战场之间传递书信，为了担心被截获后被敌人了解到自己的战略意图，信的内容往往会用双方事先约定好的一套保密的规则来撰写。二战的时候，盟军也正是通过破译敌人的密码，实现了著名的诺曼底登陆。事实上，密码学很多技术的进步都是源自于战争的推动。

到了网络时代，出于信息安全保障的需求，密码学在商业实践中变得重要起来。在信息社会，即便别人复制了我们的秘密信息，我们也很难有所察觉，因为手上的信息并没有丢失。由于数字文档很容易被修改，所以我们的重要文件也存在被他人篡改的风险。此外，如果有人将我们的秘密信息通过邮件发送给第三者或者公开发布在社交网站上，也会给我们带来很大的麻烦。

为了解决上述问题，我们开发出形形色色的基于计算机网络的密码技术，这就是现代密码学存在的根源。本质上，它是我们为防止网络信息不受控的被窃取、修订或者扩散而开发的安全风控技术。为了大致了解密码学的全貌，我们需要知道一个叫做“密码学家的工具箱”的东西。

在各个种类的密码技术中，有六种发挥着尤其重要的作用，我们将这几类技术统称为密码学家的工具箱，它们分别是：对称密码；公钥密码；单向散列函数（哈希函数）；消息认证码；数字签名；伪随机数生成器。

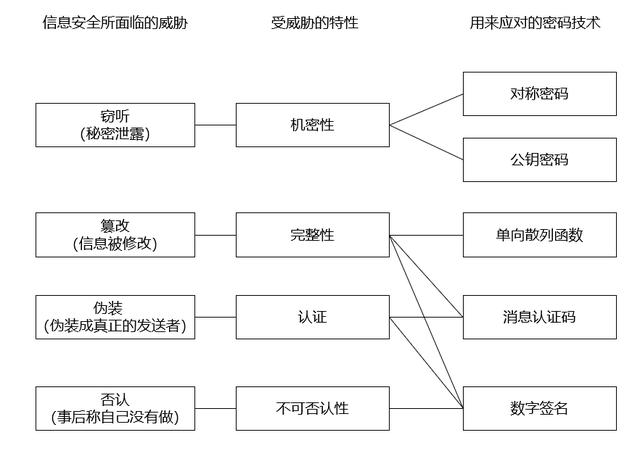
以上说法出自布鲁斯·施奈尔的《网络信息安全的真相》一书，我们可以用上面的图示来说明它们在信息世界中发挥的作用。讲到这里，我们当中对于区块链有所了解的人应该能够找到一些最近经常会遇到的词汇，接下来让我们分别来加以说明。

第一个工具是对称密码技术，简单来说就是共享密钥的密码，这时候加密方和解密方使用相同的密钥，采用这种方式的风险是需要解决密钥配送的问题。这就好比文件的加密密码是123456，解密者需要打开文件，就需要也知道这个信息，但是如何能够让解密者在绝对安全的状态下获知密码是123456呢？

虽然可以通过事先了解的方式比如二人约定个见面地点交换信息，或者指定一个密钥分配中心来分别告知双方等，以及采用类似Diffie-Hellman密钥交换等更为复杂的方法，但都存在一定的问题。密码学的专家们因此发明了一种通过公钥密码来解决密钥配送问题的技术并广受欢迎，也就是我们常说的非对称密码。

这就是第二个工具公钥密码技术，这种技术将密钥分为加密密钥和解密密钥两种。其中加密密钥一般是公开的，因此该密钥被称为公钥；相对的，解密密钥是绝对不能公开的，只能由你自己来使用，因此被称为私钥。

在公钥密码中，使用者需要生成一个包括公钥和私钥的密钥对，其中公钥会被发送给别人用于对信息加密，接收者仅需使用与之匹配的私钥就可以解密信息。由于配送给对方的公钥是公开的，这样即使在过程中被窃取也没有关系，这就解决了对称密码中的密钥配送的问题。

在公钥密码出现之后，其被广泛应用于各类信息加密领域，我们还可以基于它构建很多对称密码技术无法实现的密码系统，比如生成去中心化的身份账户、以及数字签名技术等，我们将在后面的文章对此进行详细讨论。

第三个工具是单向散列函数，它有一个输入值和一个输出值，其中输入被称为消息，输出被称为散列值（音译为哈希值）。单向散列函数可以根据消息的内容计算出散列值，散列值也被用来检查消息的完整性。通过使用该函数，即便是确认几百MB大小的文件的完整性，也只要对比很短的散列值就可以了。

在案件侦查中，办案人员会用到指纹。通过将某个特定人物的指纹与犯罪现场遗留的指纹进行对比，就能够知道该任务是否与案件存在关联。针对计算机网络上的信息，我们也可以运用到类似的“指纹”，当需要比较两条信息是否一致的时候，我们不必完整地对比消息本身的内容，只要对比它们的“指纹”就可以了。散列值就是能够反映这种信息关联性的指纹。

单向散列函数有四个主要的属性，首先是可以根据任意长度的消息计算出固定长度的散列值，其次是能够快速计算出散列值，再次是消息不同散列值也不同——两个不同的消息产生同一个散列值的情况称为碰撞，难以出现碰撞的性质被称为抗碰撞性，密码技术中所使用的单向散列函数，都需要具备抗碰撞性。最后是必须具备单向性，它指的是无法通过散列值反算出消息的性质。

单向散列函数是密码学非常核心的组成部分，我们可以使用它来确认自己下载的软件是否被篡改。比如现在很多互联网软件会把通过单向散列函数计算出的散列值公布在官网上，用户在不同的渠道下载到软件之后，可以自行计算散列值，然后与官网上公布的散列值进行比对。

通过散列值，用户可以确认自己所下载到的文件与软件作者所提供的文件是否一致。此外，在构造消息认证码、数字签名和伪随机数生成器的过程中，也都需要用到该函数。通过在加密场景中使用单向散列函数，可以节约计算机处理的时间，也可以保证生成信息的不可预测性等等。

*文章为作者李凯龙原创独立观点。 未经授权， 禁止擅自转载。

（作者：劫波李凯龙，内容来自链得得内容开放平台“得得号”；本文仅代表作者观点，不代表链得得官方立场）