spss主成分分析图解释（SPSS主成分分析指标权重值计算真的不难）

1

指标权重计算确定的困惑

相信很多写过或者正在写指标处理类论文的朋友都曾对如何计算指标权重充满困惑，到底是用熵值法，还是主成分分析法？或者其他各种看起来奥妙无穷却难以上手操作的神奇方法？好不容易确定要选用主成分分析法时又开始发愁要如何实现呢？

听说过要可以用SPPS，可是又如何使用SPSS操作呢？用SPSS进行主成分分析之后又要如何得到最终的权重呢？接下来笔者将以一个实际的案例，带领大家一步步从SPSS入手，进行主成分分析，并利用主成分分析的结果最终得到各指标的权重值。

2

利用SPSS实现主成分分析

1. 数据标准化

（1）为什么要对数据进行标准化处理

在对数据进行主成分分析前，首先要对数据进行标准化，之所以要对数据进行标准化，是因为各种类别的数据间的度量不同，比如计算经济的指标，我们通常会选取地区GDP生产总值和第三产业产值在GDP中的比重，GDP产值以亿为单位，通常以千计或万计，而第三产业产值在GDP中的比重的取值范围在0~1之间，如何能够相提并论呢？能够因为前者的数据远远大于后者，而得出前者的指标更为重要的结论吗？显然是不行的，所以要进行主成分分析，首先要对数据进行标准化。

（2）数据标准化的方法

为什么要关心数据处理的方法呢？在实际操作中，笔者曾经遇到一个问题。笔者利用SPSS自带的数据标准化方法对数据进行了标准化处理，但在权重的计算过程中不断出现负值，后来笔者几次重新调整指标类别，终于得出了均为正值的权重。但笔者最终的目的是要进行耦合协调度，这时候出现了大量的负值，而耦合度及耦合协调度的取值范围应该在0~1之间，因此笔者开始从头探索出错的原因。终于，笔者找到了原因，那就是数据标准化的方法选取的不正确，因此笔者重新选择了极差法对数据重新进行标准化，并最终顺利得到了后续的结果。

本文中笔者将先直接利用SPSS对数据进行标准化，进行主成分分析，并计算权重。随后再利用极差法对数据进行标准化并进行主成分分析，计算权重。

在这里先列出极差法数据标准化的方法：

首先要区分指标的正负向，即指标数值越大对主体产生的结果是越好还是越坏。

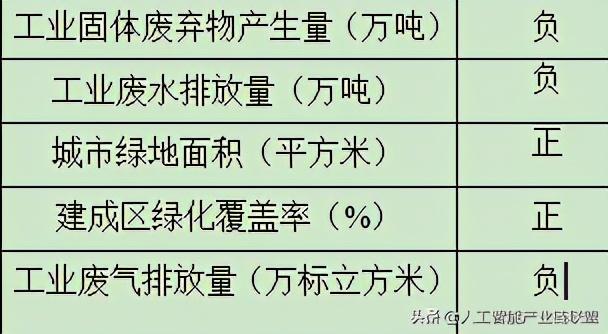
如上图，城市绿地面积越大对城市环境越好，而工业废气排放量越大，对城市环境越坏，因此城市绿地面积为正向指标，而工业废气排放量为负向指标。

2. SPSS数据标准化

（1）数据选取

我们选择广东省2016年21个市级行政区域的五项指标数据，如下图所示：

（2）SPSS中的数据标准化

首先将数据直接粘贴到SPSS数据视图中：

发现表头那里是自动生成的标号，在“变量视图”中进行修改：

这时候在数据视图可以看到表头已经修改：

这时候开始进行数据标准化处理，也很简单，点击【分析】——【描述统计】——【描述】

将选中数据放入右侧“变量”，将左下角“将标准化得分另存为变量（Z）”，这一步一定不能缺少，否则无法在变量视图中展现标准化的数据

直接点击确定，不用管输入的内容，直接看回“数据视图”，发现新增加了五列数，这些就是用SPSS标准化处理后得到的数据。

（3）主成分分析

首先什么是主成分分析？如何进行主成分分析？由于数据之间可能会具有相关性，即可能表达的是同样的含义，因此需要的对这些相关性的数据进行降维处理，用较少的变量去解释原来资料中的大部分变量，将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。通常是选出比原始变量个数少，能解释大部分资料中变量的几个新变量，并用以解释资料的综合性指标。简单来说就是，把给定的一组相关变量通过线性变换转成另一组不相关的变量，这些新的变量按照方差依次递减的顺序排列。利用SPSS极大的简化了以上过程：

点击【分析】——【降维】——【因子分析】

将刚才标准化得到的数据项添加到“变量中”：

接下来，点击：【描述】——选中“原始分析结果”，“系数”，“KMO和Bartlett球形度检验”（用来检测是否适合使用主成分分析）

点击：【抽取】——【主成分分析】，其他选项默认

点击：【旋转】——选择“最大方差法”，“旋转解”（也可以选择无，在某些情况下数据会出现异常结果，这时会需要进行矩阵旋转）

点击：【得分】，选择“显示因子得分系数矩阵”（对于权重计算来说这必不可少）

点击：【选项】，其他选项可默认

当一切设置完毕之后，点击“确定”，就可以得到主成分分析结果了。

我们主要关注【解释的总方差】和【成分矩阵】，这也是后面计算权重所不可缺少的。通常解释的总方差需要超过80%，说明提取的两个总方差对总体方差的贡献率高。从笔者分析的结果来说，好像并不适合进行主成分分析。这其实是由于数据标准化选择不可造成的，有的情况下权重计算还可以得出负值，这就是为什么要选择数据标准化的方法，而不能够只依靠SPSS中的数据标准化。相信这也困惑了很多的朋友，怀疑自己选取指标体系的合理性，在后面笔者使用极差法对数据进行标准化处理后，解释的总方差接近95%。

成分矩阵在后面全之后结果的计算中，是不可或缺的。

由于篇幅的原因，接下来利用极差法对数据进行标准化以及权重的计算将放到明日首条进行。后面在得出指标权重后，笔者还将分享如何进行多个指标系统之间耦合度及耦合协调度的方法，相信这也曾经难倒了不少朋友，笔者希望能为大家解决一些障碍，降低各位的时间成本。请大家蹲好明日首条内容哦~

荐：

【中国风动漫】除了《哪吒》，这些良心国产动画也应该被更多人知道！

声明

来源：CSDN，人工智能产业链联盟推荐阅读，不代表人工智能产业链联盟立场，转载请注明，如涉及作品版权问题，请联系我们删除或做相关处理！

,