多边形推导过程（多边形重心）

所谓重心，是一个物理学概念，指的是一个物体，它所受的所有重力会合成一个合力，这个合力的方向当然是竖直向下的，于是合力必经过一个定点，这个定点就是重心。

说得好高端，好没有烟火气。

换个说法，重心，就是整个物体的质量都理想化地集中到一个点上，这个点就是重心。

很显然，如果将物体悬挂起来，悬挂点和重心的连线必垂直于地面。

很显然，如果在物体的重心上顶一个针尖，物体能平衡稳定地放在针尖上。

我以前的物理老师告诉我，我们可以用悬挂法求重心。就是将物体挂起来，从悬挂点作竖直线，再换个悬挂点将物体挂起来，从悬挂点再作竖直线，两条竖直线的交点就是重心。

数学老师告诉我，三角形的重心就是三条中线的交点。

这些我都懂。

那么，如何求任意一个多边形的重心呢？

我们从简单的性质入手。

一个点的重心就是点本身。

两个点的重心在连接两点的线段上。

如图，设点A,B的质量分别为m,n，AB的重心为C

则在点C放一个针尖，将能够使得线段平衡

即m⋅AC=n⋅BC

所以，

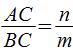
也就是说说，重心与质点的距离，与质点的质量成反比。

有了这个性质，我们就可以用数学手段求任意多边形的重心了。

对于一个三角形ABC

我们可以先求出线段AB的重心，也就是AB的中点D，点D的质量为2

于是，点C,D的重心G在线段CD上

即点G为CD靠近D的三等分点。

我们也可以用另一个方法求。

显然，AB的中点为D，BC中点为E

则重心在中线CD，AE上，

即CD与AE交点为重心G

然后，我们继续研究更多边的多边形。

一个四边形ABCD，我们可以用上面两个办法分别求重心。

方法一，

先看三角形ABC，我们可以求出其重心E，重心E的质量为3

则两点DE的重心G在线段DE上

即重心G在线段DE的靠近E的四等分点上。

方法二，

将四边形ABCD分成两个部分AB和CD，

分别求出重心E,F，连接可得直线EF

再将四边形ABCD分成两个部分AD和BC，

分别求出重心E',F'，连接可得直线E'F'

那么重心G为直线EF和E'F'的交点

解决完三角形、四边形，我们可以总结出求任意n边形重心的两个基本套路。

套路一、求出n−1边形重心G，再增加一个点的重心，为靠近G的n等分点。

套路二、用两种划分方法将多边形分成两部分，分别求重心，连线，则重心是两条连线的交点。

,