芝诺悖论深度解读（我竟然破解了芝诺悖论）

首先先问大家一道题来解释一下芝诺悖论：

人与乌龟距离10m，人每秒走2m，乌龟每秒走1m，问人什么时候能追上乌龟？

相信很多四五年级的小学生都知道，10s时就能追上。用10m÷（2m/s-1m/s）＝10s就行了。

可是芝诺非要说追不上，还找出了证据来了。他是这样解释的：

当人走到乌龟开始时的位置，乌龟走了5m，当人再走到乌龟的位置时，乌龟又走了2. 5m，到了最后，人和乌龟之间有一个无限小的距离，但是人却始终追不上乌龟。

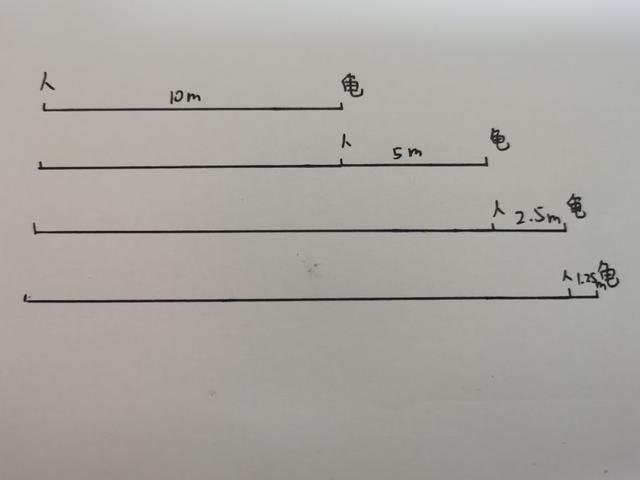
官方的解释则是给出了一个长度：普朗克长度。普朗克长度就是最小的长度，即不存在无尽小。当人和乌龟之间的距离为一个普朗克长度时，下一刻人就能超过乌龟。

对于这个解释大家一定是不太认可的，下面就看我对此的理解。

首先规定两个宇宙。第一个是主宇宙，主宇宙上的物体以跳跃的方式移动，举个例子，人每秒走2m，在这个宇宙中的定义为人瞬间消失，一秒钟之后出现在2m外。这个宇宙就像电影的胶卷，分为每一帧地运动。这个宇宙看似荒缪，但实际上我们就生活在这个宇宙之中，或者说我们的思维处在这个宇宙中。我们常用的单位m/s就是这种宇宙的产物，即每秒跳跃到X米之外。我们做数学题用的都是这种思想。

另一个宇宙是芝诺宇宙，这个宇宙中没有停止，物体始终存在并且是匀速的移动。还是那个例子，在这个宇宙中的解释就是人在一秒钟之内一直存在着且移动到2m外。

这两个宇宙的区别看似不大，但实则很大。主宇宙没有时间段的概念，你可以知道物体任意一个时刻所在位置，但是这些是无法连续起来的。芝诺宇宙中没有时刻的概念，你可以看到物体运动的完整过程，但是你无法知道具体某一时刻是所在的位置。

必须要知道的就是这两个宇宙是独立存在的，且不能有一点联系，下文会讲如果这两个宇宙之间发生联系会有多么严重的后果。

回到这道题，我们可以换一种方式表示这道题，在代入两个宇宙中。

这是根据题意画的一次函数图像。

人和乌龟在（10，20）相遇。

把它代入主宇宙中，可以理解为在十秒之内，人跳跃了20m，乌龟跳跃了10m，最终相遇了。

把它代入芝诺宇宙中就有的说的了。

可以这样理解，B坐标为（0，10），P从B点出发，在线段BA上运动，Q从O点出发，在线段OA运动，PQ永远平行于BO，BO长为10，PQ长就是人和乌龟之间的距离。

这可以判断出△APQ相似与△ABO（点是一一对应的，但是打不出相似符号）但是在芝诺宇宙中，只是无法确定每一时刻的位置，但运动也会停止，所以也是会相遇的，即A、P、Q三点重合。

由此可见，芝诺是错误的。回去再看一遍芝诺的解释，就会发现他的错误，即在芝诺宇宙中用了时刻的概念，这让两个宇宙发生了联系，从而改变了现实。这就是两个宇宙发生联系的后果。

以上为正推法，或许会有错误，但是双宇宙的概念是值得大家思考的。

下面就是比较容易理解的倒推法。

假设芝诺所说的观点正确，即不会相遇。根据相对运动，可以理解为人要运动到10m外，速度为1m/s，而人永远不能远动到哪里。但是我们把中点的概念改变一下，即人要运动到5m外，人是运动不到的，芝诺悖论的条件无法达到，就产生了矛盾了，由此证明了芝诺的错误。

不管怎么说，生活在几千年前的芝诺能留下这样一道题来，还是能看出芝诺的伟大的。另外芝诺并不是不知道他们会相遇，只是想到了另一种可能而提出来悖论，他是很伟大的。

最后再来一点小彩蛋 ，是我六年级时证明的无限不存在。

众所周知，圆的半径和直径的数量都是无限的。圆可以由半径沿一个端点旋转360度形成，也可以由直径沿中点旋转180度形成。根据这个可以得出半径数量为直径二倍，列出方程就是x＝2x。解出方程为x＝0，即无限＝0，但是用脚想都知道无限不等于0，所以无限不存在。

好了本期内容就到这里，感谢各位的阅读，如果没看懂可以多看几遍，看到了可以用本文的思想去解释一下芝诺的另一个悖论“飞矢不动”，欢迎各位在评论区留言。本文欢迎各位转载，但是请注明原作者：淩夏真。