数学x和y的关系（x是位置还是位移）

​

​一、教材分析

​位置与位移，是高中物理中的基础概念，高一物理开篇第一章就介绍了这对概念。

从内涵区分而言，两个概念的区别不难辩分：位置是指空间中的一个“点”，是状态量；位移是指空间中的一段“线段”，而且是有方向的“线段”，即从初位置指向末位置的有向线段，是过程量。

两概念之间的联系也不难理解，特别是建立空间坐标系进行理解显得浅显易懂。

​

​

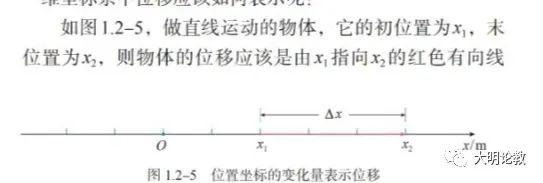
时刻与时间，也是这样一对概念，通过时间轴易容易理解时刻与时间两概念的内涵区别与外延联系。

然而，不管是位置与位移，还是时刻与时间，这两对概念在具体情景中，却时常混淆不清。 这到底是为什么呢？

例如，关于“x—t”图象的名称问题，学术上一直有讨论，讨论的焦点从纠正逻辑瑕疵向可能导致的逻辑思维障碍方向转变。新教材编写，显然注意到了这些讨论，并在教材编写时注重了“准确性”方面的校准。

​

从这一段描述可以看到，位移—时间图像，本质上就是位置—时间图像；若0时刻对应的位置，即“初始位置”（简称“初位置”），“选作坐标位置的原点”，t时刻所对应的位置坐标值与位移值恰好相等。正是基于这样的结果，位置—时间图像称为位移—时间图像也就不存在逻辑上的不自洽了。

但是，务必要注意到：称之为“位移—时间”图像时，前提条件是初位置选作为了坐标位置的原点。否则，“位置”绝不能用“位移”一词代替。

另外，号主也认为，“位置—时间”搭配是不当的，应该称之为“位置—时刻”。当然，“位移—时间”搭配是合理的。号主曾经指导过教育硕士撰写并发表过相关论文。号主在本公众号上也写过类似主题推文：

两类比值法定义物理量的不可通约性及其特殊联系性|教研分享系列249

然而，在平常教学时，也包括很多教辅书籍中，并没有注意到前述问题——在图像中，时常混淆位置与位移、时刻与时间两个概念，最终导致逻辑上的不自洽，在公式表示和图像表示之间的切换过程中，时常呈现思维障碍。 下面举例说明。

​二、题目举例

题目如下：

​

题目①中的x—v^2图像，纵坐标x，题目称之为位移，然而根据文字描述，x恐怕不能称之为位移，理由如下：题目称物块从静止开始沿x轴做匀变速直线运动，速度为零时，显然“位移”为零，然而图像显示，此时的“位移”不为零，而是“—2m”。

显然，x称之为“位置（坐标）”，前述逻辑不自洽问题就自然消除了。

本题为图像辩识题，解决此类题的关键是，根据情景描述推理写出坐标物理量之间的函数关系。

物块从静止开始做匀变速直线运动，学生很容易联想到速度—位移公式，并写成：v^2=2ax。

学生写出上面公式后，可能就“发懵”了，图线并非如此啊！学生不能辨析位置与位移两个概念，更没有纠正题目错误的习惯，于是陷入了解题困境中。

注意到，匀变速直线运动公式，事实上也描述了“两个时刻”的状态关系：

①速度—时间关系

事实上是两个时刻的速度关系，设t0时刻对应的速度为v0，t1时刻的速度为v，并令t1—t0＝t，则有v＝v0 at。

②位移—时间关系

事实上是两个时刻的位置关系，设t0时刻对应的位置坐标为x0，t1时刻的速度为x1，并令t1—t0＝t，x1—x0＝x，则有 x＝v0t 1/2•at^2

③速度—位移关系

事实上是两个位置的速度关系，设x0时刻对应的速度为v0，x1时刻的速度为v，并令x1—x0＝x，则有v^2—v0^2＝2ax。

教材在编写上面关系时，事实上特别令t0＝0，x0＝0，即有t1＝t，x1＝x，这就非常巧妙地把状态关系与过程关系统一了起来，大大地降低了学习难度。然而，如此简单化处理，存在弄巧成拙之嫌，面对图像问题和多过程问题时，由于缺失“还原”教学，学生对上面三个公式的运用，时常出现思维障碍，表现为思维僵化，思维不具有灵活性。

可见，不管是公式，还是图像，在本质上都是表示了两个状态之间的关系。对于运动图像而言，几乎可以确认，描述的是两个状态量之间的关系。从这个意义上而言，图像中的x均指位置坐标，t均指时刻，v均指瞬时值；对于运动公式而言，有时候不关心t0、t1、x0，x1状态值，仅仅关心时间t（＝t1—t0）和位移x（＝x1-x0）与它们对应“端点”（两个时刻或位置）的（瞬时）速度之间的关系，这时的运动公式更多地体现出“过程量”的关系。

总之，如果对运动图像和运动公式做到如上深入理解，并能灵活处理，那么图象问题、多过程问题就显得非常简单了。

就以本题为例，令t0＝0，初位置坐标为x0（由图可易知x0＝—2m），t1（t＝t1—0）时刻对应位置坐标为x，速度为v，则有：v^2＝2a（x-x0），即x＝x0 1/2a•v^2，根据图象不难知道a＝0.5m/s^2，继而明确v＝at，x-x0＝1/2•at^2关系，据此可以快速解题了。

由于时间关系，就写到这。明天再举一些题例进行讨论，以便于更全面而深入的反思，并促进对教材的理解与认知升华，促进审题与解题能力的提升。