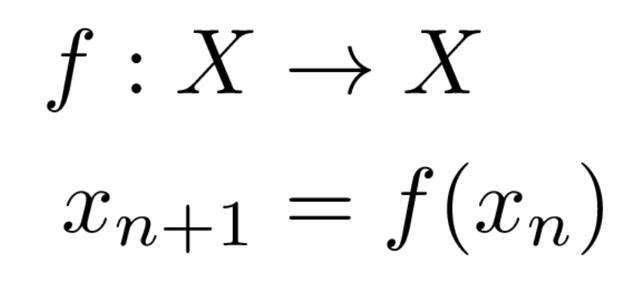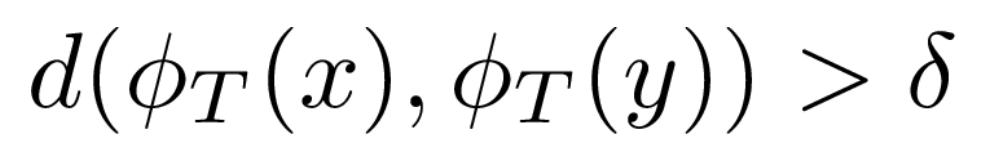数学分析中的最核心的定理（数学中最具争议的领域之一）

混沌理论可能是数学中最具争议的领域之一。因为没有人能就混乱到底意味着什么达成一致。主流媒体对蝴蝶效应的定义是：

在巴西，一只蝴蝶扇动翅膀就能在德克萨斯州引发龙卷风

这意味着，只要对一个系统做一个非常小的改变，就会导致结果会有很大的变化。

不幸的是，就像数学中的大多数事情一样，事情从来没有那么简单。蝴蝶效应用于证明对初始条件的敏感依赖，混沌系统的三个要素是：

1. 对初始条件的敏感依赖
2. 拓扑传递性
3. 密集的周期轨道

在本文中，我们将探这三个要素，并了解混沌真正的含义。

动力系统

如果你已经了解了动力系统，请跳过这一节，开始阅读关于初始条件的敏感依赖性。

当我们谈到一个系统时，我们指的是一个动态系统，它有两种形式：连续时间系统和离散时间系统。

用常微分方程定义连续时间系统。

这里f是一个足够好的函数并且可能依赖于某个参数。

从f映射到f的空间称为相空间。为简单起见，我们将假设相空间可以配备度量d（即一种测量点之间距离的方法），然后可以引入拓扑（在大多数情况下，相空间是欧几里得空间的一个子集）。

假设相空间中有给定值x_0，我们可以用ₜ(x₀)表示该值在t时刻的流量。如果我们给定初始条件，那么我们将得到初值：

它具有解x（t），然后将流定义为ₜ（x₀）= x（t）。我们将不考虑流存在条件的细节。

我们稍后会需要，周期轨道的定义，所以最好在这里定义。点x轨道的集合是：{ₜ(x), 对于任意时间t} 。也就是说，对于某个t值，流将以循环方式返回到初始条件，并将永远重复这个循环。例如，地球绕着太阳转（忽略那些细节），地球将会绕回它的起点。

我们可以对离散时间系统进行类似的讨论。在这种情况下，我们考虑以下控制方程：

x_0在n处的迭代是fⁿ(x₀)，对于一些n，fⁿ(x₀)= x₀，是一个周期轨道。

现在来看有趣的东西！

初始条件敏感依赖

这可能是三种条件中最直观的一种，当你试图将其与混沌联系起来时，这也是最合理的，同时也是混沌理论第一个被发现的部分。

在20世纪50年代和60年代，计算机的商业化实现了更快速更复杂的计算。受益的领域之一是数值天气预报。爱德华·洛伦茨参与了该领域的研究工作，并配备了皇家McBee LGP-30，用来通过一组复杂的ODE模拟天气情况。将所得序列输出为十二个数字。

为了能再次看到结果序列，他会写下之前发生的那一行数字，然后下一次，他将从中间开始的那些初始条件开始。

不过奇怪的事情会发生：他不会再看到同样的结果了。读出一开始是一样的，然后突然之间不再像预期的那样。

• 这是洛伦茨方程的解的x值，它的条件是：ρ = 28，σ = 10，β = 8/3。尽管这些点开始非常接近，但它们最终的表现完全不同。

实际发生的是，计算机内部有6位的精度，但打印出来的只有3位。这种舍入误差意味着初始条件略有不同，但这些差异造成了系统行为的巨大变化。

他发现了初始条件的敏感依赖和并诞生了混沌理论。

初始条件的敏感依赖的定义是存在一个正的delta，使得对于相空间中的所有x和x的邻域N，我们可以找到一个在N中的一个y和时间T，使：

这个方程适用于离散或连续系统。这意味着如果你给我一个初始的起始条件，我可以找到一个任意接近起始点的点，它的轨迹有一定的不同。

这在文献中有时被称为对初始条件的弱敏感依赖，因为它只是说轨迹在某一点上一定是不同的。有一种更强烈的观点认为，轨迹必须在某一时刻以指数速度发散。

这个定义是不够的。以迭代加倍映射为例：

这里的第n项是在初始条件下对D进行n次迭代。很容易看到，仅仅因为一个初始条件x₀，第n个项是xₙ= 2ⁿx₀。因此给任何两个初始条件₀x和y₀，由此产生的轨迹发散成倍增长。

因此，虽然加倍映射对初始条件敏感，但它在正实线上的表现并不十分明显。我们需要更强的条件!

初始条件的敏感依赖的一个很好的例子是双摆。我不会严格地证明它证明了初始条件的敏感依赖，因为这证明篇幅太长了。相反，我将向你们展示由Dirk Brockmann提供的精彩动画。

正如你所看到的，这两个钟摆从几乎完全相同的地方开始，但在一段时间后表现完全不同。

拓扑传递性！

我们已经确定，仅仅对初始条件敏感是不够的混沌的。我们需要更强的条件。我们想要概括运动是“到处都是”的思想。要求一个点不能停留在它的起始位置的局部，并且它被抛出去探索整个相空间是合理的。

这就是拓扑传递性的概念发挥作用的地方。它说给定一个开放集，它最终会与所有其他开放集相交。用符号写，它是这样的：

​现在我还没有定义集合的流的含义，我相信你可以通过使用一个点的流的定义来理解它。同样，这个定义没有提到它是连续映射的流还是离散映射的流，因此两者都可以应用。

这意味着，给定相空间的一个区域和足够的时间，它会通过任何其他区域。同样的，U的轨道在X上是密集的。

拓扑传递性的一个非常直观的例子就是贝克变换。它的灵感来自于面包师揉面的过程。

我们认为迭代是拉伸单位正方形，然后将其切成两半，然后将一半放在另一半之上，就像下图这样：

• 贝克变换的动画

如果你长时间盯着它看，你就会相信每个集合最终会被分散到任何地方，从而展示出拓扑的可传递性。

密集的周期轨道！

可以说，这是最容易理解的。如果有一个周期轨道，那么它在相空间是密集的。密集意味着相空间中的任意一点，都有一个周期点（周期轨道上的一点）任意地靠近它。

以一种迂回的方式，这确保了有许多非周期行为。由于在X的任意子集中，存在一个不稳定周期点的密集集合（不稳定性由初始条件的敏感依赖和拓扑传递性保证），这会导致大量的非周期行为，这正是我们在混沌系统中所期望的。

NB 1：非周期的意思是不周期性的。

NB 2：很多人不同意这点。我将在下一节中对此进行讨论。

讨论

这里给出的混沌系统的定义是由R. L. Devaney提出的，它是最广泛和普遍接受的定义之一。

已经证明，在离散时间情况下，如果相空间是一个非有限度规空间，那么实际上是拓扑传递的，周期轨道的密度意味着初始条件的敏感依赖。

正如我在本节开始时提到的，混沌有许多定义。彼得·史密斯认为，德瓦尼的定义是混沌的结果，而不是一个真正的定义本身。

• 如果离散映射具有拓扑熵，那么它就是混沌的
• 如果一个离散映射的全局Lyaponov指数为正，那么它就是混沌的
• 如果离散映射在某一点将单位间隔映射成马蹄形，那么它就是混沌的

您可能会注意到，所有这些定义都讨论离散映射，这是因为您始终可以使用称为庞加莱区域从连续地图构造离散地图。庞加莱区域使你可以减小系统的尺寸并将其离散。

如果连续系统是混沌的，那么在庞加莱区域的动力学将是混沌的。

所以现在你知道了！我认为最吸引人的地方之一是，与许多数学不同，它没有明显正确或合理的定义——它纯粹是描述物理现象。直接的结果是，对于混乱到底是什么有许多相互矛盾的概念。

,