高中数学直线方程秒杀技巧（一张思维导图帮你快速搞定高中数学直线与方程）

高中数学《直线与方程》这章非常重要，它是后面解析几何的基础，所以大家务必引起重视，建议学完后立马复习。本文，我们将这一章内容整理成了一张思维导图，希望能够帮助大家快速搞定《直线与方程》的所有核心知识点。

直线与方程-高中数学思维导图

如果大家看到上面内容大纲后，能够想起所有重要知识点，则可以略过后续内容。

直线倾斜角和斜率、直线位置关系部分重点内容，我们在思维导图中以蓝底白字显示出来了，如下图所示。

直线的倾斜角与斜率、两直线的位置关系

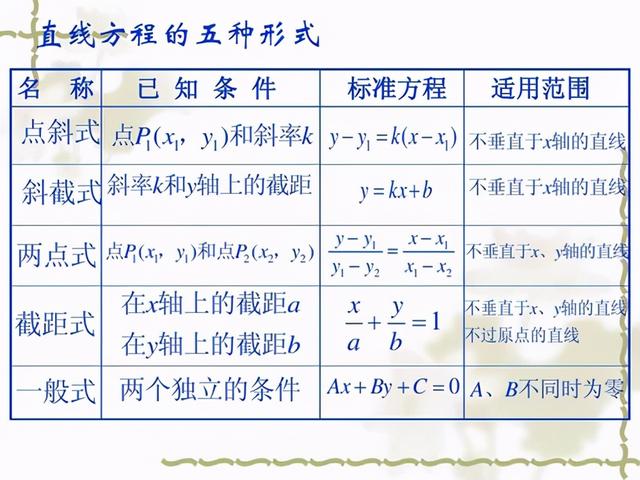
直线方程的五种形式-高中数学思维导图

补充：

①截距：横截距、纵截距，截距不是距离，是一个数，可正可负可为0；

②几种特殊位置的直线方程：

x轴：y=0；y轴：x=0；平行于x轴的直线：y=b；平行于y轴的直线：x=a；

过原点的直线：y=kx 或 x=0。

③直线和一元二次方程的相互关系：

平面内的任何一条直线的方程都是关于x、y的二元一次方程；

任何一个关于x、y的二元一次方程都表示一条直线。

④常用直线方程的设法：

A、过定点（x0，y0）直线斜率存在时，设为y-y0=k(x-x0)；直线斜率不存在时，设为x=x0；

B、与Ax By C=0平行的直线方程设为Ax By C'=0（C'≠C）；

C、与Ax By C=0垂直的直线方程设为Bx-Ay D=0；（因为斜率积为-1，故交换系数位置，还要变号）

D、过l1：A1x B1y C1=0，l2：A2x B2y C2=0的交点的直线方程设为A1x B1y C1 λ（A2x B2y C2）=0（不包括l2），也可先求出l1与l2的交点再按A处理。

直线的交点坐标与距离公式-高中数学思维导图

直线关于直线的对称：

①若已知直线l1与对称轴l相交，则其关于l的对称直线l2必然也交于这点，再在l1上面找一点关于l的对称点，即可通过两点求出l2；

②若已知直线l1与对称轴l平行，则其关于l的对称直线l2到l的距离等于l1到l的距离，且l1与l2斜率相等或斜率同时不存在。

本文，我们就分享到此，下一篇我们会分享《圆与方程》，喜欢的记得点个关注。