圆是由封闭曲线围成的（在理论里一个粗糙的圆）

一个粗糙的圆，是多边形还是圆？这个问题本身没有太大意义。毕竟，圆的定义即同一平面内，到定点的距离等于定长的点的集合；不完美、粗糙的「圆」本身就不是数学定义的圆。

图1

「粗糙」的概念是模糊的，无法为我们带来任何好处，除非我们改用更严谨的语言。

例如：「一块半生不熟的牛排，是生的牛排还是熟的牛排？」

这个问题是不是特别流氓？

我们很快就能看出，牛排不止有「生」、「熟」两种状态。

为了讨论「半生不熟」，我们要引入更严谨的描述：零分熟、一分熟、二分熟、……、八分熟、九分熟、十分熟。（没错，我列出了偶数分熟的牛排。我坚定地认为，数值化是翻译什么rare, medium well时候的伟大改进，把定性描述改成了定量描述。现实煎牛排时，不可能完美控制熟度，存在随机噪音，所以用不到无限精度的实数，浮点数 精确到小数点后三位就绰绰有余了。）

回到这个问题，我们可以提出一个类似的思路：「这个二维形状，有多接近一个完美的圆形？」

在二维空间中，它是圆度（roundness）。

图2

对于圆度，我们大致可以把它看做内切圆与外接圆的比值。更具体的数学推导，可以参见英文维基、ISO等更专业的网站。另外，圆度和圆度误差不是同一个东西，百度百科的简介里似乎搞混了。一个完美圆的圆度为1，圆度误差为0。

我们可能会觉得，只要一个图形从各个角度测量的直径都一样，那么它就是一个圆形。其实不是这样，定宽曲线（例如莱洛多边形）了解一下？

在三维空间中，类似的概念是球度（sphericity）。但是，球度并非圆度在三维空间的直接推广。

球度是Compactness measure of a shape的一个例子（这里的compact和拓扑学没有任何关系）。它的计算方式为

，其中Ap是三维物体的表面积，Vp是该物体的体积。

维基百科Sphericity - Wikipedia列出了一些常见三维几何体的球度：

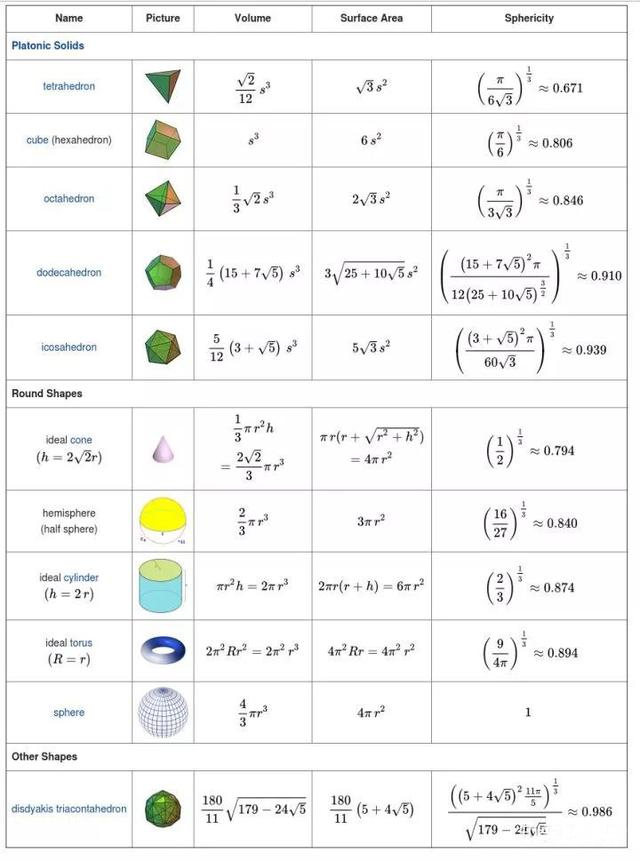
更深入的相关知识，估计要找地质学或者工程专业（大概吧……）的工作者了解了。

注：本文转自公众号“数学职业家”