出租车的正确开法（学点出租车几何学）

出租车几何学

再也不用担心堵车了

今天超模君下班回家的时候，明明半个小时的路程，愣是堵车堵了一个半小时才到家。

一说起堵车这个世界性难题，北上广深的模友应该都深有感触（心塞ing）。所以经常有人调侃：在大都市生活，一天的时间，要么在上班，要么堵在上班的路上。看来交通问题是令所有大都市管理者都头疼的大难题！

那么今天，超模君就给各位模友分享一篇有关出租车几何学问题的文章，希望能给主管或研究大都市交通设计规划问题的模友一个启示。

这篇文章从一个独特的视角为求解城市道路问题提供了一个新思路。文章有点长，我们一起来看看吧。

作者：

钱有华 浙江师范大学数理信息学院

崔继峰 内蒙古工业大学理学院

张峰铭 浙江师范大学数理信息学院

摘要：两点之间的距离是连接两点的最短路径的长度，在欧几里得平面几何中，这条路径就是连接两点的线段。但是，在以方格布局为主的城市街道中，两点间最短的路径就可能不再是线段了，我们把这种新的路径称之为出租车距离。本文中我们将介绍出租车几何学中的距离公式、圆、垂直平分线等知识，并运用这些知识解决城市建设布局中的一些实际问题，探讨其在教学当中的意义和重要性。

1 引言

改变欧几里得几何学中的一条或多条公设，将有可能构建各种非常独特的几何学，它们都如同我们熟知的平面几何一样，是符合自然规律的，是没有内在矛盾的。这些非欧几里得几何中的某些流派在现代的物理学和宇宙学中非常有价值的，例如在宇宙空间中或原子核世界里，罗氏几何更符合客观实际；在地球表面研究航海和航空等实际问题时，黎曼几何更准确一些。但是它们往往是非常难以理解和构想的，所以绝大多数非专业人士无法对其进行研究。然而在众多的非欧几里得几何中，有一门特殊的几何学被人们称之为出租车几何学，或者曼哈顿距离。这门几何学极易理解，只需利用普通的方格纸，任何人都可以探讨其结构，享受发现新定理的乐趣。这一体系可以用出租车漫游城市来模拟，城市的街道只有水平和竖直两个方向，并且以每个街区为单位形成的方格大小相等。

我们试想一下Eugene F. Krause在《Taxicab Geometry》[1]书中提出的三个真实生活问题。第一，在一座理想的棋盘式布局的城市中，警察局的调度员收到信息，有一个突发事故发生在X=(-1,4)处。而在该地区附近有两辆警车，A车位于(2,1), B车位于(-1,-1)，那么应该派哪辆车前去处理事故？第二，在此理想城市中有三所高中，A校位于(2,1)，B校位于(-3, 3)，C校位于(-6,-1)。绘制一个学校的管辖范围，让理想城市中的每一个学生都能到离他们最近的学校去上学。第三，一个电话公司要设立公用电话亭，使方圆12个街区的市中心每过4个街区就能找到一个公用电话。由于资金紧张，电话公司希望设立尽可能少的公用电话亭。那么到底需要多少个电话亭，它们的位置又在哪里？

让这些问题变得有趣的是，我们必须沿着城市街道建设的限制来解决它们，而不能把它们看作能在天上飞。这就是说我们熟悉的欧几里得距离公式已经不适用了，而出租车几何学就是用来解决这方面问题的方法。

在文[2]中提到，出租车几何学首先是由闵可夫斯基（Hermann Minkowski）提出的，这位数学家出生于俄罗斯，曾在瑞士苏黎世当过爱因斯坦少年时期的老师，后来为狭义相对论提出了经典的四维时空公式。大约在上一世纪之交，闵可夫斯基在德国刊行了其选集，他在书中详细分析了各种度量体系，例举了在不同空间中为了满足度量空间的公理而定义的不同的测量距离方法。在众多的度量方法中就包含出租车度量，并且它的距离公式一直沿用到当今的出租车几何学中。然而直到1952年，Karl Menge在芝加哥科学与工业博物馆召开的一个几何学术展览上，出租车几何学才得以正式命名。在展览中发放的一本名叫“You Will Like Geometry”的宣传册里第一次提到了“出租车”几何学。

在出租车几何学发展的这100多年中，既有被人们忽视而停滞不前的时候，也有受到注重并广泛应用的时候，而如今对这门几何学的研究已经有了很大的成就，并得到了全面的应用。这有以下的几个原因：

第一，出租车几何学与欧几里得几何学非常相似，并且容易理解。它可以被认为是一个度量系统，其中点代表理想城市中水平和竖直街道的交叉点（所有街道都是双向可行的）。从早前对出租车几何学的研究来看，它非常适合大学生进行学术研究。

第二，出租车几何学很适合进行几何理论的研究。它既可以用由David Hilbert提出的综合法研究[3]，也可以用由George David Birkhoff提出的度量法进行研究[3]。还有第三种方法是利用几何学中的抽象群和群论[3]，这种方法是FelixKlein和Arthur Cayley提出的，他们认为研究几何应该通过让运动群在给定的集合中活动。另外，一些出租车几何学中关于二次曲线的命题已经得到了证明。

第三，出租车几何学的实际价值在于其在城市交通建设、道路规划等方面的广泛运用。我们可以看到出租车几何学是非常有用的城市地理模型，只有在天上飞的鸟才会认为城市中两幢大楼的距离是一条直线，对于人们来说出租车距离才是真正的距离。而在我们熟悉的国际象棋里，也同样运用到了出租车几何学的原理。在下象棋的过程中，车（城堡）是以出租车距离来计算棋盘格上的距离；而王（国王）与后（皇后）使用切比雪夫距离，象（主教）则是用转了45度的出租车距离来计算（在同色的格子上），也就是说它以斜线为行走路径。只有国王需要用一步一步走的方式移动，皇后、主教与城堡可以在一或两次移动走到任何一格（在没有阻碍物的情况下，且主教忽略它不能走到的另一类颜色）。

在本文中，我们主要讨论一些出租车几何学的基本知识，并运用这些知识解决现实生活中的实际问题，探讨其在教学方面的意义。

2 出租车几何学的基本性质

2.1 两点间的距离

出租车几何是一个度量体系，其中拓扑空间的点就是相当于方格纸上水平线与竖直线的交点，亦即理想城市中街道的交点。如果A、B两点在同一条街上，那么它们之间的距离同欧几里得几何一样，只要数出它们之间相隔多少个单位就行了。但是如果A、B不在同一条街上（不考虑单行道限行），如图2-1所示，

图2-1 纽约曼哈顿区部分地图

此时就不能用经典的欧几里得距离公式来计算从点到点的距离

在欧几里得几何中两点之间直线最短，但在出租车几何中两点之间可能会有很多种路径，并且他们都是最短的。所以计算点到点的距离就是点A到B的一条最短路径构成的平行或垂直于x轴的线段，我们用下面这个公式计算：。

即两点的横坐标之差与纵坐标只差的绝对值的和。回到图2-1中，我们令点A为原点，以

为X轴，为y轴，以每个街区为一个单位长度，建立直角坐标系。那么点A的坐标为（0,0），点B的坐标为（3,3），可以得到点A到B的出租车距离为

所以我们必须至少走过6个街区才能从点A到达点B。

出租车几何学距离公式是一个对度量的合理定义，因为它满足度量的公理：

(1)非负性：任两点A和B，都有一非负实数|AB|与之对应，该实数就叫做点A到点B的距离。当且仅当这两点重合时，距离d（A,B）=0。

(2)对称性：d（A,B）=d（B,A）。

(3)三角不等式：对于任意不共线的三个点A，B和C，有。

这也就是说出租车几何学是建立在一个合理的度量空间上的。

证明：

令点、和。

公理（1）非负性

如果A=B，那么

如果，那么或，

并且或。

假设，那么

因此。

公理（2）对称性：

公理（3）三角不等式：

令A、B、C三点非共线，那么它们可以构成一个三角形。

因此。

证毕。

这个公式还可以推广到n维的情况。在出租车距离中，两个向量P，Q在n维固定的笛卡尔坐标系统的矢量空间中的距离，等于点在坐标轴上的投影线段长度的总和，也就是

，

当向量。

在欧几里得几何中，两点之间的最短距离（直线距离）是一条唯一的直线，但在出租车几何里，存在很多条最短路径。如图2-2所示，绿线为欧几里得几何中唯一的最短距离，其长度为。而红、黄、蓝三条线则均为出租车几何中的最短距离，且它们的值都为12。

图2-2 最短距离下的多条路径

对于不在同一街道上的两个点，到底有多少这种路径,我们可以借助著名的帕斯卡三角（杨辉三角）来解决。现在让我们回到图2-1，将图中的A、B两点看作一个33矩形的对角顶点。图2-3中的细线表示如何在帕斯卡三角中作矩形来解决这个问题。在矩形的下角我们可以找到答案：A、B之间共有20条不同的路径。（注意帕斯卡三角是左右对称的，因此无论将矩形往哪一侧画得到的结果都是一样的。）

图2-3 帕斯卡三角

我们知道帕斯卡三角可以得出从较大的r元集合中选出n元集合有多少种不同的方法，所以我们只要看该三角形的第n条对角线与第r行交叉点处的数字就可以知道答案。在图2-1的问题中，20便是6样东西中选出3样的不同方法数。这里3对应矩形的一边，6则对应矩形的两边之和。20也就是出租车从33矩形的一角行驶到对角的不同路径的总数。

在出租车几何学中，为了决定两点之间的路径数，不一定要去画帕斯卡三角。我们也可以利用熟知的组合数公式来计算从r件物品中选取n件的方法总数，即

。

例如在图2-1的问题中，r!等于1×2×3×4×5×6，即720，n!等于1×2×3，即6，而(r-n)!等于1×2×3，即6，从而根据公式得出N=720/36=20。

在帕斯卡三角形中，矩形可以向两个方向中的任意一侧倾斜，这可以从图中直接得到证实。从较大的r元集合中选取n元的方法总数，等同于从r元中选取r-n元的方法数，这一事实在直观上是显而易见的，因为一旦从r元中选出一个n元的集合，便会有独一无二的r-n元集合剩下来。在出租车几何学中意味着，如果在方格纸上画出一个欧几里得矩形，那么在矩形的两个对角顶点之间的不同的出租车路径数同另外两个对角顶点之间的不同路径数完全一样。

2.2 圆

2.2.1 概述

在欧几里得平面几何中，圆被定义为“到某定点的距离等于定长的点的集合”，这个定点就是圆心，定长是半径，直径是圆中任意两点间最长的距离并且等于半径的两倍，周长是圆的边的长度。圆心坐标为(a,b)半径为r的圆可以表示为。

然而在出租车几何中，圆就变得非常有趣了。我们仍然沿用欧几里得几何中对圆、圆心、半径、直径和周长的定义，但把距离换成出租车距离，得到的圆就完全不同了，此时圆心坐标为(a,b)半径为r的圆可以表示为。

如图2-4，是圆心坐标为(0,0)半径为4的圆。

图2-4 出租车几何中的圆

图2-5 非出租车几何中的圆

意外的是，运用不同的度量方法得到的圆居然完全不一样。在出租车几何中，我们得到的更像是一个正方形。但如图2-5中的“正方形”就不是一个圆了，我们可以看到图2-5中圆心的坐标为（0,0），到点（4,0）的距离是4，而到点（4,4）的距离却是8。因此根据定义到某定点的距离等于定长的点的集合，只要正方形的边平行于平面坐标轴就不再是圆了。考虑到平面中y轴的正方向是指向北方，x轴的正方向是指向东方，那么圆的四个顶点必须要在正东、正南、正西、正北方。

欧几里得几何中规定不重合的两个圆的交点不能超过两点，但两个出租车圆可以相交于任意个有限个数的点[4]，如图2-6。圆越大，它们的交点就越多。这也就得出在出租车几何中任意三个不在同一条直线上的点是不能确定一个圆的。

图2-6 两个出租车圆的交点

2.2.2 圆的周长

猜想：出租车几何中圆的周长可以用半径的函数来表示。

圆的周长是圆一周的长度，在欧几里得几何中我们可以用公式C=2πr来计算（r表示半径）。在出租车几何中我们可以经过测量得出表2-1的这些数据。

表2-1 半径与周长

半径r	周长C
1	(2)(4)=8
2	(4)(4)=16
3	(6)(4)=24

从一个顶点到下一个连续的顶点的距离是圆的半径的两倍。（这也就意味着当等腰直角三角形的一条直角边在水平方向上时，斜边不再等于直角边的倍，而是直角边的2倍。）由此可以推出一个关于周长和边的等式

C=4a。

其中a表示边的长度。用2倍的半径代替边的长度，就得到下面这个关于周长和半径的等式

C=8r。

2.2.3 圆的面积

猜想：出租车几何中圆的面积可以用半径的函数来表示。

在欧几里得几何中，计算圆的面积的公式是。在出租车几何中我们处理边的长度需要用出租车距离，上面曾提到过，半径为4的圆它的一条边的出租车距离是8。但是我们在计算面积时如果把它当做正方形，用边的出租车距离来算似乎不太合理，这样就会计算出64个单位的面积，经过在图中的简单观察和计算就可以推出个假设是不成立的。所以即使是圆已经变成了正方形，我们也不能用古典的欧几里得方法计算面积。

让我们考虑用水平和竖直的长度来计算面积，面积被定义为图形表面的单位方格数。出租车圆可以被分为四个全等的等腰直角三角形，并且每个三角形的底和高都是r，如图2-7。注意到计算面积的公式是在底和高分别在水平和竖直方向的基础上得出的，所以底和高的长度就是欧几里得几何中的长度。

图2-7 出租车几何中圆面积的计算

每一个三角形的面积是

，

乘于全等三角形的个数4，就得到圆的面积为

。

有趣的是这个结果与在欧几里得几何中的结果是一样的。在欧几里得几何中正方形的边长为，而正方形的面积。

另外，该公式也可以改写成面积与出租车圆的边长的等式。边长等于半径的两倍，在之前的公式中，用a=2r替换r，得到

。

2.2.4 π的大小

在欧几里得几何中被定义为平面上圆的周长与直径之比值，

。

在出租车几何中，我们仍沿用欧几里得对的定义，而根据上面的计算周长C=8r，此时

。

所以在出租车几何中圆周率不再是无理数了，而是有理数。

2.3 点到直线的距离

2.3.1 点到直线的距离的计算方法

在欧几里得平面几何中，有一种标准的方法计算从一个点A到直线l的距离。如图2-8，首先过点A做一条垂直于l的直线，则l与相交于点B。那么点A到直线l的欧几里得距离就是点A到点B的距离，即

。

图2-8 欧几里得几何中点到直线的距离

然而在出租车几何学中，由于距离的度量方法发生了巨大的改变，所以我们很难用一个标准的方法来计算点到直线的距离。但是我们可以用点A到直线l上任意一点的最短距离来表示点A到直线l的距离[1]，即。

那么如何找到这个距离最短的点P呢？我们可以用画同心圆的方法，如图2-9，圆心为点A的出租车圆半径不断扩大，直到圆的边与直线相交。我们先考虑图2-9-I的情况，注意到点到线的距离其实是从点到直线的竖直距离。但是这也许是因为这条线比较平缓（直线的斜率的绝对值小于1）。如果线比较陡会怎样？在图2-9-II中直线的斜率的绝对值大于1，此时点到线的距离是从点到直线的水平距离。考虑直线的斜率为1（或-1）的情况，如图2-9-III，在这种情况下由于圆与直线的交点不止一个，所以我们有无限多种路径可以用来计算点到直线的距离。因此，线的斜率大小会影响到点的距离的计算方法。

图2-9 用出租车圆解决点到直线距离的问题

让我们总结一下出租车几何中计算点到直线距离的方法：

（1）如果直线的斜率的绝对值小于1，用点到直线的竖直线段测量距离；

（2）如果直线的斜率的绝对值大于1，用点到直线的水平线段测量距离；

（3）如果直线的斜率的绝对值等于1，用点到直线的水平或竖直线段测量距离。

2.3.2 垂直平分线

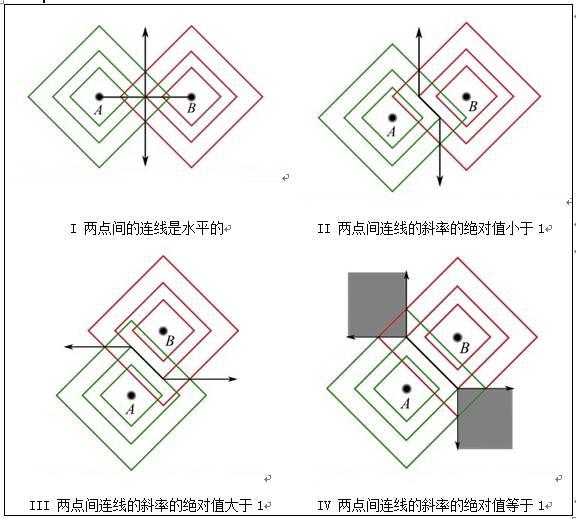
我们知道线段的垂直平分线为“到两端点距离相等的点的集合”，是一条直线，然而到了出租车几何学中就不同了。我们需要分四种情况讨论，这主要是取决于两个不断扩大的出租车圆是如何相交的，如图2-10。

图2-10 垂直平分线

在第一种情况中，如图2-10-I，你会发现它与欧几里得几何中的垂直平分线没有区别。当连接两点的线段是水平或竖直的时候，起初两个扩大的出租车圆是相交于一点的，即连接两点的线段的中点，但随着圆的不断扩大，它们最终会相交与两点。这就产生了同欧几里得几何一样的垂直平分线。

如果连接两点的线段不是水平或竖直的，结果就不同了。起初两个扩大的出租车圆会相交于一条线段，并且这条线段会穿过连接两点的线段的中点，如图2-10-II。随着圆的不断扩大，它们最终会相交与两点，形成2条射线。注意，这种情况又可以分为两种子情况，即两个不断扩大的圆的交点所形成的射线会根据连接两点线段的不同斜率而有不同的朝向。图2-10-II是斜率绝对值小于1的情况，而图2-10-III则是斜率绝对值大于1的情况。

最后还剩下连接两点的线段斜率的绝对值等于1的情况，如图2-10-IV。在这种情况下，两个扩大的出租车圆起初也会相交于一条线段，但随着圆的不断扩大，两个圆会继续相交于线段，而不是点。这就形成了两个分别在对角线上的区域。

总之，只有在连接两点的线段是水平或竖直的时候，垂直平分线才是条直线。而在别的情况下，垂直平分线可能是一条折线，甚至有时候连线都不是，但和欧几里得几何相同的是，它始终穿过连接两点的线段的中点。

3 出租车几何学的实际应用

从文[6][7]中我们可以看到，在现实生活中两个地方最短的距离无论是通过汽车、火车还是飞机都不会是直线，而是出租车距离。并且城市的规划也离不开出租车几何学，从历史的角度来看，我们主要有两种类型的城市：自然发展的城市和经过规划的城市。自然发展的城市往往发展得比较缓慢，并且注重于维护它的自然景观，街道、建筑、花园等零星分散，也没有固定的形状。而规划过的城市是根据人口的增长而发展和规划的（根据统计学的方法分析出生率和死亡率来预测），它的发展模式更加趋向于竖直和水平的区域发展，即更符合出租车几何学。从上世纪60年代起，城市的建设的重心就开始从注重艺术的美感转为了注重格局和效率。所以当今大多数城市的规划都涉及到了使用几何模型和数学模型，出租车几何学更是运用到了城市布局、道路规划、距离测算等各个方面。

虽然对于城市的规划，出租车几何学是优于欧几里得几何学的数学模型，但是它也并不是完美的。因为它是建立在很多假设和对城市的简化上的，例如城市的街道必须沿着东西或南北走向，街道不能有弯曲的弧度，建筑物被看作是一个点等等。显然现实生活中这样的理想城市是不存在的，城市建设还要受限制于它所处的地理环境，并方便人们出行。但不得不说大多数城市的大部分区域与这些假设并没有太大的差异，所以我们从理想城市中研究出来的结果可以被运用到现实的城市当中。况且用数学建模的方式解决现实生活中的问题，本来就需要通过假设来简化一些细节，如果没有这些简化，数学模型就会变得非常庞大并且难以解决，甚至有时候我们都无法把问题转换为数学模型。

下面我们就用序言中提到的三个现实问题来举例说明出租车几何学的实际应用。

3.1 警车派遣

在一座理想的棋盘式布局的城市中，警察局的调度员收到信息，有一个突发事故发生在X=(-1,4)处。而在该地区附近有两辆警车，A车位于(2,1), B车位于(-1,-1)，那么应该派哪辆车前去处理事故呢？

解:警车行驶时不能穿过人们的房子，它们必须沿着规划的道路来走，所以出租车几何学是解决这个问题的最好方法。我们只需要比较两辆警车到事故发生地点的出租车距离，就可以得到结果。首先建立直角坐标系,如图3-1。

图3-1 建立直角坐标系

事故发生地点X到车A的距离为：

事故发生地点X到车B的距离为：

综上所述，车B更靠近事发地点，所以调度中心应该派B车前去处理事故。

3.2 学校范围设定

在理想城市中有三所高中，A校位于(2,1)，B校位于(-3, 3)，C校位于(-6,-1)。绘制一个学校的管辖范围，让理想城市中的每一个学生都能到离他们最近的学校去上学。

解:在这个问题中，学生上学需要沿着街道来走，所以我们应该采用出租车几何学。首先建立直角坐标系,如图3-2。

图3-2 建立直角坐标系

为了确定学校的边界我们可以用画两点之间的垂直平分线的方法，因为垂直平分线上的点到线段两端点的距离总是相等的，这样就能保证学生到学校的距离最短。下面我们分别画出线段AB、BC和AC的垂直平分线，可以用2.3.2中提到的方法来作图，如图3-3。

图3-3 三条线段的垂直平分线

从图3-3中我们可以看到，学校A的范围应该是线段AB和AC的垂直平分线所划分的四个区域中包含A的区域。根据垂直平分线的定义，我们不难理解，只有在垂直平分线上的学生到两个学校的距离才相等，如果偏向其中的任意一个学校，那么他到该校的距离就小于到另外一个学校的距离，所以应该去该学校上学。同理，学校B的范围就应该是线段AB和BC的垂直平分线所划分的四个区域中包含B的区域，而学校C的范围应该是线段BC和AC的垂直平分线所划分的四个区域中包含C的区域。图3-4即为最终结论。

图3-4 结果

3.3 电话亭分布

一个电话公司要设立公用电话亭，使方圆12个街区的市中心每过4个街区就能找到一个公用电话。由于资金紧张，电话公司希望设立尽可能少的公用电话亭。那么到底需要多少个电话亭，它们的位置又在哪里？

解:因为人们不可能穿过大厦，越过房屋，所以我们用出租车几何学来解决这个问题。首先，在直角坐标系中作一个以原点为圆心，半径为12的出租车圆。然后，将这个出租车圆分为半径为2的小出租车圆，这样每个小圆就代表4个街区，总共得到36个小圆。如图3-5。

图3-5 街区划分

我们可以看到，从图3-5中的点(12,0)出发走过四个街区有三个点，分别是(8,0)，(10,2)和(10,-2)，而从(10,2)和(10,-2)出发再走过四个街区得到的点都包含(8,0)。现在我们来看(8,0)这个点，作以它为圆心，以4为半径的出租车圆，那么只要在这个圆中的所有点，到达(8,0)的距离都小于等于4。所以我们可以在点(8,0)设置一个公用电话亭，它的服务范围就是以它为圆心4为半径的圆，只要在这个范围内，用最捷径的方法至多走4个街区就能找到一个公用电话亭。依照这样的设定，以原点为圆心，半径为12的出租车圆就被划分成了9个半径为4的圆，如图3-6。在这9个圆中，我们在每个圆的圆心都设立一个电话亭，那么在方圆12个街区的市中心每过4个街区就能找到一个公用电话亭。

图3-6 结果

综上所述，这家电话公司总共需要设立至少9个公用电话亭，它们的位置如图3-6，每个红点分别代表一个公用电话亭，且坐标分别为(8,0)，(-8,0)，(0,8)，(0,-8)，(4,4)，(-4,4)，(-4,4)，(-4,-4)，(0,0)。其他方法详见文[8]。

4 出租车几何学的教学意义

在大学的数学教育中，每个学生都有自己的兴趣和擅长的方面，同学们对同一个概念的理解也可能不同。所以引入类似出租车几何学这样的知识体系，可以大大发挥不同学生的不同能力和优势，发散他们的思维，并培养他们的创新创造能力。正如一些数学教育专家说的那样，大学课程对于几何的基础教育需要引入一些不同于传统的欧几里得几何平面的例子，这样才能使学生学会处理不同公理下的几何。我们通常学习的知识都是有连贯性的，但是学习数学并不是一个连续的过程，有时也需要打破一些固有的知识体系和思想模型，这样才能得到思维上的突破和知识上更深入的理解。详见文[3][9]。

我们学习知识，同时也是一个再创造的过程。打个比方,你的手上有一副扑克牌，你会以为它一定是用来打桥牌的吗？肯定不会，它也可以用来玩接龙、二十一点、德克萨斯扑克等游戏，甚至在有些文化中还可以用来算命。桥牌和接龙的区别并不在于扑克牌，而是出牌的规则。同样的扑克，人们可以根据自己的喜好来选择规则，从而进行完全不同的扑克游戏。所以人人都可以在原有的基础上发明新的游戏，创造新的规则。同样地，在数学当中也是这个道理。出租车几何学就是在古典的欧几里得几何学的基础上，改变了其对两点距离定义而得到的。这样就给每个同学一个探索和发现的机会，去开辟新的数学世界。

提出问题被看做是数学思维的一个重要组成部分。近年来，数学的教学越来越强调给予学生机会来提出问题。有研究表明，通过学生自己提出问题的教学方式可以很大程度的培养学生自主解决问题的能力，并提高他们对数学学科的兴趣。然而这样的教学模式也需要一些条件：第一，需要创造一个适合提问的环境；第二，老师要引导学生提出一些有意义有价值的问题。而出租车几何学就给同学们了一个很好的提问平台，因为在这块领域还有很多未知的问题等待人们去探索发现。

从近年来看，各地的中等教育系统也在逐步引进出租车几何学这个概念[10]。我们可以看到2010年广东省高考理科数学试卷的最后一道大题就是关于出租车几何学的，题目为：

设是平面直角坐标系xOy上的两点，现定义由点到点的一种折线距离ρ（A,B）为

，

对于平面xOy上给定的不同的两点,

（1）若点C（x，y）是平面xOy上的点，试证明；

（2）在平面xOy上是否存在点C（x，y），同时满足

①ρ（A,C） ρ（C,B）=ρ（A,B）

②ρ（A,C）= ρ（C,B）。

若存在，请求出所有符合条件的点，请予以证明。

在这道题目中，出题人引入了出租车几何学中的距离公式，并以这个距离公式为背景，求解平面中三个点的关系。类似的题目还出现在2009年上海市高考理科数学试卷的填空题当中，也是以距离公式为背景考两点间的距离。我们发现这两道题目都是以压轴题的方式出现在高考试卷当中，可见出租车几何学在高中教学方面还是有一定影响的。这主要得益于：第一，其概念简单容易理解，符合现实的生活情况；第二，与我们所学习的欧几里得几何不同，同学们对其比较陌生，有一定的难度。

在以大学为主的高等教育中，由于缺乏相应的学科和课程，同学们可以通过学术论文或者毕业论文的形式来自主研究出租车几何学。特别是一些基础理论方面的知识，例如圆、椭圆、双曲线等二次函数，然后再延伸到一些特殊方面的应用。这些理论相对比较简单，又富有挑战性。

在此，我们引入一种非常简单的方法来学习出租车几何学，那就是运用一款知名的电脑游戏“模拟城市”（SimCity）。在这款游戏中玩家以城市规划者的身份，在以出租车几何学为背景的方格地图上，建设布局整个城市的建筑设施。同学们可以在游戏的过程中，慢慢体会出租车几何学的奥秘。如果你还想进行一些更加深入的研究，不妨在游戏中加入一些限制，比如选址建立一个医院使得它到附近三个居民社区的距离最短，或者每过两个街区设立一个便利商店并且要求便利店的总数最小。详见文[11]。

5 延伸

5.1 类出租车几何学

出租车几何学可以容易地推广到三维或更高维的整数格点[12][13]，但是对于其他种类的格点，例如有限或无限的三角形或六边形格点上的出租车几何学，仍然是一片未开垦的土地。另外，格点也未必需要局限在平面上，它们也可以定义在柱面、球面、环面、莫比乌斯带、克莱因瓶乃至你所喜欢的任何东西之上。只要始终遵守一条原则：你的驾驶员坚持在街上开车，永远走最短路径，把你送到要去的地方。下面我们就来研究一下在三角形格点中的类出租车几何学。

我们知道，正方形并不是一个严格的几何图形，只要在左边或右边轻轻的一推它就会变成一个菱形。如果这种现象发生在方格的坐标平面内，那么x轴的正半轴与y轴的正半轴的夹角就会变成60°，并且我们画出单位菱形中的较短的那条对角线，这样就得到了一种三角形格点的类出租几何学坐标系。此时我们仍定义点的坐标为投影到对应的x轴与变形的y轴的长度。

在这种几何学中，点A到点B的距离根据其在坐标轴的不同位置可以分为三种情况。为了研究他们的距离公式，我们需要对坐标平面做一些改进，引入除了x轴、y轴之外的第三个坐标轴y′轴。y′轴就是由上面提到的由单位菱形中的较短的那条对角线所形成的，它与x轴和y轴均为60°夹角。这三个坐标轴把平面分成了六个等大的象限，我们用一至六来顺序标记从x轴的正半轴与y轴的正半轴所形成的象限开始逆时针数的象限，如图5-1。平面中的任意一个点都有三条分别平行于坐标轴的直线穿过。那么任意两个点的连线可能有四种情况：在第一和第四象限，在第二和第五象限，在第三和第六象限，平行于坐标轴。

图5-1 类出租车几何学坐标平面象限划分

在此，三个距离公式分别是:

（1）如果两个点在第一和第四象限，如图5-2-I。那么

；

（2）如果两个点在第二和第五象限，如图5-2-Ⅱ。那么

；

（3）如果两个点在第三和第六象限，如图5-2-Ⅲ。那么

。

图5-2 距离公式分类

如果两点的连线平行于x轴，那么它适用于公式（3）；如果两点的连线平行于y轴或y′，那么它适用于公式（2）。

这也是一个对度量的合理定义，因为它满足第二节中提到的度量的公理。

5.2 等价度量

设X是一个非空集合，ρ是X上的一个非空度量。以X上的所有球形邻域为基的拓扑称为自由度量ρ所诱导出的X上的拓扑。在非空集合X上也许可以定义出若干个不同的度量，由这些不同度量可以分别诱导出X上的若干个拓扑。如果在同一个集合上的两个度量和诱导出了同一拓扑，那么和是X上的2个等价度量。如果X上两个不同的度量和所诱导出的X上的拓扑相同，或在同一个拓扑空间X上可以分别定义与其拓扑相容的两个不同的度量，那么会给我们处理问题带来很大的便利，因而度量的等价性是非常值得关注的。

定义：集合X上的两个度量和称为等价的，如果X的子集A是度量空间中的开集当且仅当A是度量空间中的开集（即和所诱导出的X上的拓扑相同）[14]。

设X，Y是两个拓扑空间。设X，Y是两个拓扑空间。如果映射 f：X→Y在任意一点x∈X处都连续，则说 f 是连续映射[15]。

例：定义使得对于任何

。

证明：

（1），都是的度量。

（2）度量空间有着完全相同的开集（意即一集合对于某一度量而言是开集，则对另一度量而言也是开集）。

（3）设为一映射，若 f 对于的度量之一而言为连续映射，则 f 对于的度量之另一而言也是连续映射[16]。

证：

（1），满足度量的非负性、对称性是显然的，下面验证它们也满足三角不等式。

设

故，都是的度量。

（2）因为（5-1）

设U为中的开集，即任意x∈U，存在ε>0，使,其中表示度量空间中的x的球形邻域。由①右边不等式，即U是的开集。

反之，设U是中的开集，即任意x∈U，存在ε>0，使,由①左边不等式，即U是的开集。

因此与有相同的开集。

又 （5-2）

利用此不等式，仿上可证，有相同的开集。因此，有完全相同的开集。

（3）不妨设 f 对于的度量ρ而言为连续映射，设U为中（对中的度量而言）的任一开集，则为中的开集，由（2），也是，中的开集。因此，f 对于的度量而言，也是连续映射。

其他两种情况类似证明。

6 结论

在本文中，我们通过介绍在出租车几何学中两点间的距离、圆和点到直线的距离等基本性质，解决了城市规划中的一些布局问题，充分展示了其在实际运用中的巨大潜力。出租车几何学是求解城市道路问题的有力工具，它提供了一个简单而精妙的途径来确保问题解决方案的可行性。我们可以看到它的教学意义也是非常显著的，在启发学生创新思维的同时，给予他们研究的广袤空间。在最后提到的两个延伸方向中，我们通过改变坐标轴夹角引出了类出租车几何学，并用等价度量的定义证明了其与欧几里得几何度量是等价的。

参考文献

[1] Krause, Eugene F. Taxicab Geometry: AnAdventure in Non-Euclidean Geometry[M]. New York: Dover Publications. 1987.

[2] Louise Golland. Karl Menger and TaxicabGeometry[J]. Mathematics Magazine,1990, 63(5): 326-327.

[3] Divjak Blaženka.Notes on Taxicab Geometry[J]. KoG, 2002, 55:5-9.

[4] 马丁·加德纳.谈祥柏、谈欣.最后的消遣[M].上海科技教育出版社,2010:141-154.

[5] Russell Euler andJawad Sadek. Theπs Go Full Circle[J]. Mathematics Magazine, 1999, 72(1): 59-63 .

[6] Chip Reinhardt.TaxiCab Geometry: History and Applications![J]. The MontanaMathematics Enthusiast, 2005, 2(1): 38-64 .

[7] 伊万·莫斯科维奇.李琳.生命的游戏[M].新兴出版社.2006:12-22.

[8] Benjamin Urland. Erratum: An Improvement onthe article Taxi Cab Geometry: History and Applications![J]. The MontanaMathematics Enthusiast, 2007, 4(1): 115-127

[9] 彭翕成.不同的公理不同的几何[J].中学数学,2011,(9):62-63.

[10] 史嘉.从一道高考题欣赏出租车几何学[J].中学数学,2011,(17):21-23.

[11]Tuba Ada and Aytaç Kurtuluş. A Study on Problem Posing-Solving in the Taxicab Geometry and ApplyingSimcity Computer Game[R]. The Mathematics Education into the 21st Century Project,Proceedings of the 10th International Conference .2009.

[12] 林诗丽. Taxicab几何的几类空间曲面[J]. 华南师范大学学报(自然科学版), 1986, 01: 11-15.

[13] Z. Akca,R. Kaya. On the Distance Formulae in ThreeDimensional Taxicab Space[J]. Hadronic Journal, 2004, 27(5):521-532.

[14] 吴红英,汪火云.度量等价与一致等价的判别[J].吉首大学学报（自然科学版）, 2009,30(4):16-18.

[15] 尤承业.基础拓扑学讲义[M].北京市：北京大学出版社, 1997:11-29.

[16] 熊金城.点集拓扑讲义[M].北京市：高等教育出版社, 2011:38-83.

作者简介：

钱有华

浙江建德人，2012年博士毕业于北京工业大学。现任教于浙江师范大学数理信息学院，副教授，硕士生导师，美国“数学评论”评论员，中国力学学会会员，国际期刊Nonlinear Science Letters A 编委。入选2007年浙江省高校优秀青年教师资助计划, 入选2013年校级优秀中青年骨干教师。研究方向为非线性动力学与控制。

Email:qyh2004@zjnu.edu.cn

崔继峰

陕西省榆林市人，2015年博士毕业于上海交通大学，现任教于内蒙古工业大学理学院数学系，美国工业和应用数学学会（SIAM）会员，硕士生导师。

研究方向：应用数学、非线性力学和非线性动力系统。

Email: cjf@alumni.sjtu.edu.cn / cjf@imut.edu.cn

张峰铭：2015年毕业于浙江师范大学信息与计算科学专业，现就读于爱尔兰都柏林大学。

本文由超级数学建模编辑整理

获作者原创授权

转载请关注公众号，回复“转载”

-----这里是数学思维的聚集地------

“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。20万数学精英都在关注！

,