神经网络为什么要进行反向传播（如何更好地理解神经网络的正向传播）

图：pixabay

原文来源：medium

作者：Matt Ross

「机器人圈」编译：嗯~阿童木呀、多啦A亮

介绍

我为什么要写这篇文章呢？主要是因为我在构建神经网络的过程中遇到了一个令人沮丧的bug，最终迫使我进入该系统，并且真正了解了神经网络的核心的线性代数。我发现我已经做得很好了，而这只需要确保两个相乘矩阵的内部维度相匹配，而当发生bug时，我只是将各自将矩阵转置于不同的位置，直到事情解决。但是其中有一个隐藏的事实，那就是我并没有真正了解矩阵乘法运算的每一步。

图1 Sigmoid函数

因此你就会获得隐藏层的每一个单元的激活。然后，你可以使用相同的方法来计算下一层，但是这次你将使用隐藏层的激活作为“输入”值。你将所有a^2激活（即隐藏层）单元乘以第二组权重Theta2，将连接到单个最终输出单元的每个乘积相加，并将该乘积通过Sigmoid函数加以计算，以获得最终的输出激活a^3。g（z）是Sigmoid函数，z是x输入（或隐藏层中的激活）和权重θ（由图5中的正常神经网络图中的单个箭头表示）的乘积。

图2 应用Sigmoid函数的假设函数

一旦你拥有这一切，你想计算网络的成本（图4）。你的成本函数本质上将计算出给出范例的输出假设h（x）和实际y值之间的成本/差异。所以，在我继续使用的范例中，y是由输入所表示的实际数字的值。如果在网络中有一个“4”馈送图像，则y就是值“4”。由于存在多个输出单元，所以成本函数将h（x）与输出相比较，相对于列向量，其中第4行为1，其余的都为0。意思是表示“4”输出的输出单元为真，其余为假。对于1，2或n的输出，请参见下文。

图3 我们的样本数据y值表示为逻辑真/假列向量

图4 多级Logistic回归成本函数

上述成本函数J（theta）中的两个Sigma将总结出你通过网络（m）和每个单个输出级（K）提供的每个示例的成本。现在，你可以通过单独进行每个计算来实现这一点，但是事实证明，人类已经定义的矩阵乘法的方法使得它能够完美地同时执行所有这些正向传播计算。我们那些专攻数值计算的朋友已经优化了矩阵乘法函数，使得神经网络可以极大地输出假设。要编写我们的代码，以便我们能够同时进行所有的计算，而不是说在所有输入示例中的for循环中运行所有内容，这是一个称为向量化代码的过程。这在神经网络中是非常重要的，因为它们的计算成本已经足够高了，我们不需要任何循环来减慢我们的运算速度。

我们的网络范例

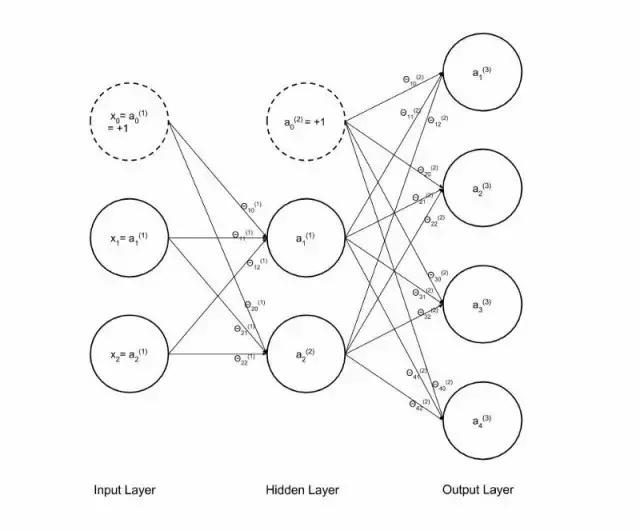
在我们的网络中，我们将有四级，即1,2,3,4，并将遍历这个计算的每个步骤。我们假设拥有的是一个已训练的网络，并已通过反向传播训练了Theta参数/权重。它将是一个3层网络（2个输入单元，2个隐藏层单元和4个输出单元）。网络和参数（又名权重）可以表示如下：

图5 具有权重的神经网络

在进一步深入之前，如果你不知道矩阵乘法是如何工作的，那就花费7分钟来看看可汗学院（Khan Academy）（https://www.khanacademy.org/math/precalculus/precalc-matrices/multiplying-matrices-by-matrices/v/matrix-multiplication-intro），然后再看一两个范例，确保你对它的工作原理有一个直观的认识。再次强调，在进一步深入研究之前了解这一点很重要。

那我们就从所有的数据开始。我们的3个示例数据和相应的y输出值。这些数据不代表任何东西，它们只是数字，用来显示我们将要做的计算：

图6 数据

当然，如上所述，由于有4个输出单元，我们的数据必须表示为一个逻辑向量矩阵，三个示例输出中的每一个都要如此。我使用的是MATLAB，以便将我们的y向量转换成一个逻辑向量矩阵：

yv=[1:4] == y; %creating logical vectors of y values

图7 样本矩阵输出y数据变为逻辑向量

另外，请注意，我们的X数据没有足够的特征。在图5的神经网络中，当我们计算权重/参数和输入值的乘积时，我们就有了那个虚线偏差单元x（0）。这意味着我们需要将偏差单元添加到数据中，也就是说我们在矩阵的开头添加一个列：

X = [ones(m,1),X];

图8 附有偏差的数据，偏差即由图5中的神经网络虚线单位/节点所指代

数据X被定义为第一个输入层a^1的第一个激活值，所以如果你在代码（第3行）中看到了一个a^1，它只是指初始输入数据。网络中每个连接/箭头的权值或参数如下所示：

图9 我们的神经网络的第一组权重/参数，其指数与图5神经网络图的箭头匹配。

下面是我们将用于计算逻辑成本函数的完整代码，我们已经解决了第2行和第9行，但是我们将在本代码的其余部分慢慢地分解矩阵乘法和重要的矩阵操作：

1: m = size(X, 1);

2: X = [ones(m,1),X];

3: a1 = X;

4: z2 = Theta1*a1';

5: a2 = sigmoid(z2);

6: a2 = [ones(1,m);a2];

7: z3 = Theta2*a2;

8: a3 = sigmoid(z3);

9: yv=[1:4] == y;

10: J = (1/m) * (sum(-yv’ .* log(a3) — ((1 — yv’) .* log(1 — a3))));

11: J = sum(J);

首先，我们来进行正向传播的第一步，第4行代码。将每个范例的输入值乘以与其相应的权重。我总是想象输入值在图5的网络中沿着箭头流动，乘以权重，然后在激活单元/节点等待其他箭头进行乘法运算。然后，特定单元的整个激活值首先由这些箭头（输入x权重）的总和组成，然后该和通过Sigmoid函数进行操作（参见上面的图1）。

所以在这里很容易犯你的第一个矩阵乘法错误。由于我们的附有偏差的单元被添加到X（在这里也称为a^1）是一个3x3矩阵，而我们的Theta1是一个2x3矩阵。由于Theta：2x3和X：3x3的两个内部维度是相同的，因此把两个矩阵相乘就变得很简单了，其结果应该是正确的，且会给出我们的2x3合成矩阵？对不起，错了！

z2 = Theta1 * a1; %WRONG! THIS DOESN'T GIVE US WHAT WE WANT

尽管运行这个计算将输出一个我们期望和需要将其用于下一步的正确维度的矩阵，但是所有计算的值将是错误的，因此所有的计算都将从这里开始表现为错误的。另外，由于没有计算机错误，所以很难判断为什么网络成本函数计算出了错误的成本，如果你注意到了，请记住，当进行矩阵乘法时，得到的矩阵的每个元素ab是第1矩阵中的行a和第二个矩阵中的列b的点积和。如果我们使用上面的代码来计算z^2，则得到的矩阵中的第一个元素将由我们的第一行Theta的[0.1 0.3 . 0.5]与整列偏差单元相乘得到，[1.000;1.000; 1.000]，这对我们没有用。这意味着我们需要将范例的输入数据矩阵进行转置，使得矩阵将每个theta与每个输入正确相乘：

z2 = Theta1*a1';

矩阵乘法的运算如下:

图10 矩阵乘法的指数符号表示。列中的结果元素表示单个示例，并且行是隐藏层中的不同激活单元。每个示例中 2个隐藏层导致两个值（或行）。

然后，我们将上述z²矩阵中的6个元素中的每个单元应用于Sigmoid函数：

a2 = sigmoid(z2);

这为我们提供了三个示例中每两个隐藏单元的隐藏层激活值的2×3矩阵：

图11 隐藏单元的激活值

因为这是作为矩阵乘法完成的，所以我们能够同时计算隐藏层的激活值，而不是在所有这些例子中使用for循环，当使用更大的数据集时，计算变得极其昂贵。更不用说再需要反向传播了。

现在我们具有第二层激活单元的值，它们作为输入到下一层和最后一层，即输出层。该层对于第2层和第3层之间的图5中的每个箭头，都有一组新的权重/参数Theta2，我们继续重复上面的步骤。将连接到每个激活节点的权重的激活值（输入）乘以连接到每个激活节点的产品，然后通过sigmoid函数运行每个激活节点和以获得最终输出。我们的a²作为我们的输入数据，我们的权重/参数如下：

图12 带指数的Theta2权重/参数。每行表示对每个输出单元贡献的权重。

我们要做以下计算：

z3 = Theta2*a2;

但是在我们这样做之前，我们必须再次添加我们的偏差单元到我们的数据，在这种情况下，隐藏层激活a²。如果你在图5中再次注意到，隐藏层中的虚线圆圈（0），仅在下一次计算时才添加的偏置单元。因此，我们把它添加到上面图11所示的激活矩阵中。

介绍我犯过的错误就是我写这篇文章的动机。要正向传播激活值，我们将Theta中的一行的每个元素与a2中的每个元素相乘，并且这些乘积的总和将给出所得到的z³矩阵的单个元素。通常，数据结构的方式是将偏差单元添加为列，但是如果你这样做（我愚蠢地做了），这将会给我们一个错误的结果。所以我们将偏置单位作为一行添加到a²中。

a2 = [ones(1,m);a2];

图13 将偏移行添加到a²激活中

在我们运行矩阵乘法以计算z³之前，请注意，在z²之前，你必须转置输入数据a 1，使其对于矩阵乘法“正确排列”，以计算出我们想要的结果。这里，我们的矩阵按照我们想要的方式排列，所以没有转置a²矩阵。这是另一个常见的错误，如果你不了解这个核心的计算，那么很容易犯这个错误（我过去对此非常内疚）。现在我们可以在4x3和3x3矩阵上运行矩阵乘法，得到3个例子中的每一个的4×3矩阵输出假设：

z3 = Theta2*a2;

图14 矩阵乘法的指数符号表示。列中的合成元素代表单个示例，并且行是输出层的不同激活单元，共有四个输出单元。在分类问题中，这意味着四个类/类别。还需要注意的是，每个元素中的所有a的[m]上标指数是示例编号。

然后我们对z²矩阵中的12个元素中的每一个元素使用sigmoid 函数：

a3 = sigmoid(z3);

这为我们每个输出单元/类提供了一个4x3矩阵的输出层激活（类似于假设）：

图15 每个示例网络的每个输出单元的激活值。如果你在所有的示例中做一个循环，这将是一个列向量，而不是一个矩阵。

从这里，你只是计算成本函数。唯一需要注意的是，你必须转置y向量的矩阵，以确保你在成本函数中正在进行的元素操作与每个示例和输出单元完全对齐。

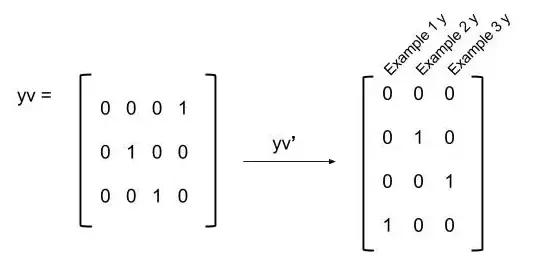
图16 逻辑y向量矩阵的转置

然后我们把它们放在一起来计算成本函数：

图4 多级Logistic回归成本函数

J = (1/m) * (sum(-yv’ .* log(a3) — ((1 — yv’) .* log(1 — a3))));

J = sum(J);

这就是我们的成本，应该注意的是以计算所有类以及所有示例的双倍总和。这就是所有人。矩阵乘法可以使这个代码非常整齐和高效，不需要让循环减慢，但是你必须知道矩阵乘法中发生了什么，以便你可以适当地调整矩阵，无论是乘法顺序，必要时进行转置，并将偏差单元添加到矩阵的正确区域。一旦你把它打破了，掌握得就更加直观，我强烈推荐，如果你仍然不确定，慢慢地像这样通过一个示例，它总是归结为一些非常简单的基本原理。

我希望这对于正向传播所需的线性代数的掌握，同时去神秘化是非常有帮助的。

原文链接：https://medium.com/@matt.as.ross/under-the-hood-of-neural-network-forward-propagation-the-dreaded-matrix-multiplication-a5360b33426

,