任意平行四边形面积最简单的算法（此题求四边形的面积）

各位朋友，大家好！今天，“数学视窗”给大家讲解一道初中数学几何综合题，这道题目非常简洁，但还是有一些难度，在做题时需要仔细思考如何合理运用给出的条件，以便找出解题思路。此题考查了面积变换，平行线分线段成比例，等高三角形的面积与底的关系等知识。下面，我们就一起来看这道例题吧！

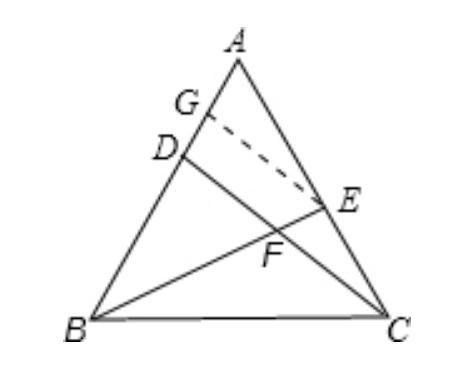
例题：（初中数学综合题）如图，在△ABC中，已知D是AB的中点，AE=2EC，BE、CD交于点F，且△ABC的面积是12平方厘米，求四边形ADFE的面积．

分析：大家想要正确解答一道数学题，必须先将大体思路弄清楚。下面就简单分析一下此题的思路：要求四边形ADFE的面积，肯定需要将面积进行转化，可以看作两个三角形的面积之差。

可以作EG∥CD交AD于G，根据平行线分线段成比例，求出EF和BE之间的关系，然后求出△CEF的面积。又知D是AB的中点，△ABC的面积是12平方厘米，即可求出△ADC的面积，最后由四边形ADFE的面积=S△ADC-S△CEF进行计算，即可得到结果．

解答：（以下的过程仅供参考，可以部分进行调整，并且可能还有其他不同的解题方法）

如图，过点E作EG∥CD交AD于G，则

AE/AC=AG/AD，（平行线分线段成比例）

∵AE=2EC，

∴AG/AD=2/3，（等量代换计算得出）

∴AG=2/3AD，DG=1/3AD，

又∵D是AB的中点，

∴BD=AD，

∴BG=BD DG=4DG，即DG=1/4BG，

∴BD=3/4BG，（等量代换计算得出）

又∵EG∥FD，

∴BF/BE=BD/BG=3/4，

∴FE=1/4BE，

（等高三角形的面积与底的关系）

∴S△CEF=1/4S△EBC，

∵AE=2EC，即EC=1/3AC，BD=AD，

△ABC的面积是12平方厘米，

∴S△EBC=1/3·S△ABC=4平方厘米，

S△ADC=1/2·S△ABC=6平方厘米，

∴S△CEF=1/4S△EBC=1平方厘米，

∴S四边形ADFE=S△ADC-S△CEF

=6-1

=5（平方厘米）

即四边形ADFE的面积是5平方厘米.

（完毕）

这道题考查了面积变换的知识、等高三角形的面积与底的关系等，解答本题的关键是作平行线，再根据平行线段成比例的知识求解。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家给“数学视窗”留言或者参与讨论。