集合的法则(集合的初步)
一.集合的概念
一般地,指定的某些对象的全体称为集合(简称为集)
集合中每个对象叫做这个集合的元素
也可以这么说(集合:把一些能确定的,不同的对象看成一个整体,就说这个整体由这些对象的全体构成的集合,构成集合的每个对象叫做这个集合的元素。)
2.集合的表示方法:
集合常用大写字母表示,如集合A,集合B......
元素常用小写字母表示,如a,b......
3.集合元素的性质
(1)确定性:集合中的元素必须是确定的
如果a是集合A的元素,就说a属于集合A,记作a∈A
如果a不是集合A的元素,就说a不属于集合A,记作a∉A
(2)互异性:集合中的元素必须是互不相同的
(3)无序性:集合中的元素是无先后顺序的,集合中的任何两个元素都可以交换位置。
例:
整体→集合
中国古代四大发明
对象→元素
造纸术,指南针,火药,印刷术
4.重要数集

例:
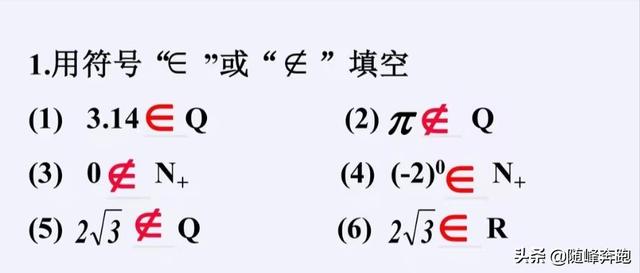
例题:
1.(5分)以下元素的全体不能够构成集合的是( )
A.中国古代四大发明 B.地球上的小河流
C.方程x2﹣1=0的实数解 D.周长为10cm的三角形
【分析】本题考查的是集合的含义问题.在解答过程中,要充分考虑几何元素的特性:互异性、确定性、无序性、丰富性.在分析师根据选项逐一排查即可.
【解答】解:由题意可知:
对A:中国古代四大发明,满足构成集合的元素的特征;
对C:方程x2﹣1=0的实数解,即﹣1、1满足结合元素的特征;
对D:周长为10cm的三角形所对应的元素,满足几何元素的特性.
而对B:地球上的小河流,则不具备确定性的特点,因为小到什么时候才算小是不确定的.
故选:B.
2.(5分)下面四个命题正确的是( )
A.10以内的质数集合是{0,2,3,5,7}
B.由1,2,3组成的集合可表示为{1,2,3}或{3,1,2}
C.方程x2﹣2x 1=0的解集是{1,1}
D.0与{0}表示同一个集合
【分析】A.质数指能被1和本身整除的正整数,举出10以内的所有质数;
B.由集合中元素的无序性,可判断;
C.由集合中元素的互异性,即可判断;
D.由元素和集合的关系,可知0属于集合{0}.
【解答】解:A.10以内的质数集合是{2,3,5,7},故A错;
B.由1,2,3组成的集合可表示为{1,2,3}或{3,1,2},它们都相等,故B对;
C.方程x2﹣2x 1=0的解集应为{1},故C错;
D.0表示元素,{0}表示一个集合,只有一个元素,故D错.
故选:B.
【点评】本题考查集合的概念,集合中元素的性质:确定性、无序性、互异性,属于基础题.
,免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。文章投诉邮箱:anhduc.ph@yahoo.com






